Matematika dan arsitektur

"The Gherkin",[1] 30 St Mary Axe, London, selesai tahun 2003, merupakan konstruksi yang dirancang secara parametrik.
Kuil Kandariya Mahadewa di Khajuraho, India, adalah contoh arsitektur religius dengan struktur fraktal yang bagian-bagiannya menyerupai keseluruhannya, selesai dibangun tahun 1030.[2]

Matematika dan arsitektur saling terkait seperti halnya seni lainnya, arsitek menggunakan matematika untuk beberapa alasan. Selain matematika yang dibutuhkan dalam teknik bangunan, para arsitek menggunakan geometri untuk menentukan bentuk ruang bangunan. Dari Pythagoras pada abad ke-6 SM, hingga seterusnya; menciptakan bentuk-bentuk yang dianggap harmonis, dalam menyusun bangunan dan lingkungannya yang sesuai dengan prinsip matematika, estetika dan kadang-kadang juga aspek-aspek religius. Menghiasi bangunan dengan benda-benda matematis seperti teselasi; dan memenuhi fungsi lingkungan, seperti meminimalkan kecepatan angin di sekitar basis bangunan tinggi.

Di Mesir Kuno, Yunani Kuno, India dan dunia Islam; bangunan termasuk piramida, kuil, masjid, istana dan monumen makam ditata dengan proporsi yang spesifik karena alasan agama. Dalam arsitektur Islam, bentuk geometris dan pola ubin geometris digunakan untuk menghias bangunan, baik di dalam maupun di luar bangunan. Beberapa candi Hindu memiliki struktur fraktal, di mana komponen-komponennya menyerupai bentuk keseluruhannya, serta menyampaikan pesan tentang kosmologi Hindu yang tak terbatas. Dalam arsitektur Tiongkok, tulou yang berada di provinsi Fujian berbentuk melingkar, dengan struktur pertahanan komunal. Pada abad ke-21, ornamen matematis juga digunakan untuk menutupi bangunan masyarakat umum.

Dalam arsitektur Renaisans, simetri dan proporsi dengan teliti ditegaskan oleh arsitek seperti Leon Battista Alberti, Sebastiano Serlio dan Andrea Palladio, yang dipengaruhi oleh karya Vitruvius yang berjudul De architectura dari Romawi Kuno dan aritmetika Pythagoras dari Yunani Kuno. Pada akhir abad ke-19, Vladimir Shukhov di Rusia dan Antoni Gaudí di Barcelona mempelopori penggunaan struktur hiperboloid di Sagrada Família, Gaudí juga memasukkan paraboloid hiperbolik, teselasi, lengkungan katener, katenoid, helikoid, dan permukaan teratur. Di abad ke-20, gaya arsitektur modern dan dekonstruktivisme mengeksplorasi berbagai geometri untuk mencapai efek yang diinginkan. Permukaan minimum digunakan semaksimal mungkin sebagai atap penutup yang berbentuk seperti tenda di Bandara Internasional Denver, sementara Richard Buckminster Fuller mempelopori penggunaan struktur kerang tipis yang dikenal sebagai kubah geodesik.

Bidang terkait

Di masa Renaisans, seorang arsitek seperti Leon Battista Alberti memiliki pengetahuan dalam banyak disiplin ilmu, termasuk aritmetika dan geometri.

Arsitek Michael Ostwald dan Kim Williams, mempertimbangkan hubungan antara arsitektur dan matematika. Perlu diperhatikan bahwa bidang yang umum dipahami mungkin tampak hanya terhubung sedikit; di mana arsitek adalah profesi yang berkaitan dengan masalah praktis dalam membuat bangunan, sedangkan matematika murni mempelajari jumlah dan benda abstrak lainnya. Tapi, mereka berpendapat bahwa kedua bidang ini sudah sangat terhubung sejak zaman dahulu. Di Romawi Kuno, Vitruvius menggambarkan seorang arsitek adalah orang yang mengenal berbagai disiplin ilmu lainnya, terutama geometri; yang memungkinkannya mengawasi perajin terampil di semua area yang diperlukan, seperti tukang batu dan tukang kayu. Hal yang sama diterapkan pula di Abad Pertengahan, di mana para lulusan belajar aritmetika, geometri dan estetika di samping silabus dasar tata bahasa, logika, dan retorika (trivium) di aula elegan yang dibuat oleh ahli bangunan yang telah membimbing banyak pengrajin. Seorang ahli rancang bangun berada di puncak profesinya, dan diberi gelar arsitek atau insinyur. Di masa Renaisans, quadrivium yang terdiri dari aritmetika, geometri, musik dan astronomi menjadi silabus ekstra yang diharapkan dari generasi Renaisans seperti Leon Battista Alberti. Demikian pula di Inggris, Sir Christopher Wren, yang dikenal saat ini sebagai arsitek pertama, yang juga seorang astronom terkenal.[3]

Williams dan Ostwald selanjutnya mengulas interaksi antara matematika dan arsitektur pada tahun 1500; di mana sosiolog Theodor Adorno, mengidentifikasi tiga kecenderungan di kalangan arsitek yang terdiri dari: menjadi revolusioner dengan memperkenalkan gagasan baru sepenuhnya; atau menjadi reaksioner, dan gagal mengenalkan perubahan; atau menjadi revivalis, yang benar-benar berpandangan mundur. Mereka berpendapat bahwa arsitek telah menghindari pembuktian matematika dalam mendapat inspirasi di zamannya. Ini akan dijelaskan tentang mengapa dalam periode revivalis, Arsitektur Kebangkitan Gothik di Inggris abad ke-19; hanya memiliki sedikit keterhubungan dengan matematika. Sama halnya, mereka mencatat bahwa matematika hampir tidak dijadikan bahan pertimbangan di periode reaksioner seperti Mannerisme di Italia yang terjadi sekitar tahun 1520 hingga 1580, atau gerakan Barok dan Palladian pada abad ke-17. Sebaliknya, gerakan revolusioner di awal abad ke-20 seperti aliran Futurisme dan Konstruktivisme secara aktif menolak gagasan lama, serta menghargai matematika yang mengarah pada arsitektur Modern. Menjelang akhir abad ke-20, geometri fraktal dengan cepat digunakan oleh arsitek, seperti halnya dalam ubin aperiodik, yang memberikan kesan atraktif dan memiliki daya tarik bagi bangunan.[4]

Arsitek menggunakan matematika karena beberapa alasan, salah satunya menjauhi penggunaan penting matematika dalam rekayasa bangunan.[5] Pertama, mereka menggunakan geometri karena geometri dapat mendefinisikan bentuk ruang bangunan.[6] Kedua, mereka menggunakan matematika untuk merancang bentuk yang dianggap cantik atau serasi.[7] Sejak zaman Pythagoras dengan falsafah angka religius mereka,[8] arsitek di Yunani Kuno, Romawi Kuno, dunia Islam dan Renaisans Italia telah memilih proporsi binaan lingkungan, yaitu bangunan dan rancangan lingkungannya—yang disesuaikan dengan prinsip matematika dan estetika, serta kadang-kadang juga aspek-aspek religius.[9][10][11][12] Ketiga, mereka menggunakan benda matematis seperti teselasi untuk menghias bangunan.[13][14] Keempat, mereka juga menggunakan matematika dalam bentuk pemodelan komputer untuk memenuhi tujuan lingkungan, seperti meminimalkan arus putaran udara di dasar bangunan tinggi.[1]

Bentuk-bentuk ruang harmonis

Estetika sekuler

Roma kuno

Denah rumah Yunani oleh Vitruvius.
Vitruvius
Informasi lebih lanjut: Vitruvius, Modul Vitruvian dan De architectura
Bagian dalam Pantheon oleh Giovanni Paolo Panini, tahun 1758.

Seorang arsitek Romawi kuno yang berpengaruh, Vitruvius, pernah berpendapat bahwa desain bangunan seperti kuil bergantung pada dua kualitas, yaitu proporsi dan symmetria. Proporsi memastikan bahwa setiap bagian bangunan terhubung secara harmonis dengan bagian lainnya. Symmetria dalam penggunaan Vitruvius berarti sesuatu yang mendekati modularitas (modularity) lebih dari simetri cermin, karena hal ini berkaitan dengan perakitan komponen (modular) ke dalam keseluruhan bangunan. Pada Basilika di Fano, dia menggunakan rasio bilangan bulat kecil, terutama bilangan segitiga (1, 3, 6, 10, ...) untuk proporsi struktur menjadi modulus (Vitruvian).[a] Dengan demikian lebar hingga panjang Basilika adalah 1:2; dengan lorong di sekelilingnya setinggi lebarnya, 1:1; kolom setinggi lima kaki dan tingginya lima puluh kaki, 1:10.[9]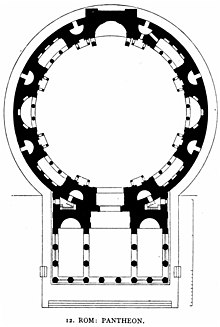

Denah lantai Pantheon.

Vitruvius menamai tiga kualitas arsitektur yang dibutuhkan dalam De architectura, pada tahun 15 SM: kekokohan, kegunaan (atau "commodity" dalam bahasa Inggris Henry Wotton pada abad ke-16), dan sukaria. Hal ini dapat digunakan sebagai kategori untuk mengklasifikasikan bagaimana cara matematika digunakan dalam arsitektur. Kekokohan meliputi penggunaan matematika untuk memastikan sebuah bangunan dapat berdiri, oleh karena itu alat matematika yang digunakan dalam desain yang mendukung konstruksi, misalnya untuk memastikan stabilitas dan pemodelan kinerja. Kegunaan sebagian berasal dari penerapan matematika yang efektif, penalaran dan analisis hubungan spasial dan hubungan lainnya dalam suatu desain. Sukaria adalah atribut yang dihasilkan dari bangunan, yang dihasilkan dari perwujudan hubungan matematis di dalam bangunan; Ini mencakup kualitas estetika, sensual dan intelektual.[16]

Pantheon
Artikel utama: Pantheon

Pantheon di Roma telah bertahan utuh, menggambarkan struktur klasik Romawi, proporsi, dan dekorasi. Struktur utamanya adalah kubah, apeks dibiarkan terbuka sebagai lingkaran okulus yang membiarkan cahaya masuk; yang berhadapan dengan barisan tiang pendek dengan pedimen segitiga. Tinggi okulus dan diameter lingkaran interiornya sama, yaitu 43,3 meter (142 ft), sehingga keseluruhan interior pas, dan tepat berada di dalam kubus, serta bagian interiornya bisa menampung bola dengan diameter yang sama.[17] Dimensi ini lebih masuk akal bila diungkapkan dalam unit pengukuran Romawi kuno: Kubahnya membentang 150 kaki Romawi[b]); okulus tersebut berdiameter 30 kaki Romawi; pintu keluar berukuran 40 kaki Romawi yang tinggi.[18] Pantheon tetap menjadi kubah beton terbesar di dunia.[19]

Abad Renaisans

Informasi lebih lanjut: Arsitektur Renaisans
Fasad Basilika Santa Maria Novella, Firenze, 1470. Dekorasi (berbentuk persegi) dan yang lebih tinggi adalah oleh Leon Battista Alberti.
Perspektif arsitektur panggung yang ditetapkan oleh Sebastiano Serlio, tahun 1569.[20]
Denah dan elevasi Andrea Palladio pada Villa Pisani.

Risalah Renaisans pertama tentang arsitektur ditulis adalah Leon Battista Alberti pada tahun 1450, dengan judul De re aedificatoria (Seni Bangunan); Ini menjadi buku cetak pertama tentang arsitektur pada tahun 1485. Sebagian didasarkan pada karya arsitek Vitruvius, De architectura dan aritmetika Pythagoras melalui Nicomachus. Alberti memulai dengan sebuah kubus, dan mendapatkan rasio darinya. Selain itu, diagonal wajah memberi rasio 1:√2, sedangkan diameter bola yang membatasi kubus memberikan 1:√3.[21][22] Alberti juga mendokumentasikan penemuan perspektif linier Filippo Brunelleschi, yang dikembangkan untuk memungkinkan proses desain bangunan yang akan terlihat indah proporsional apabila dilihat dari jarak dekat.

Teks utama berikutnya adalah karya Sebastiano Serlio berjudul Regole generali d'architettura (Aturan Umum Arsitektur); volume pertama muncul di Venesia tahun 1537; volume 1545 (buku 1 dan 2) mencakup geometri dan perspektif. Dua metode Serlio dalam membangun perspektif adalah salah, tetapi hal ini tidak menghentikan karyanya yang telah banyak digunakan secara luas.[23]

Pada tahun 1570, Andrea Palladio menerbitkan buku yang berjudul I quattro libri dell'architettura (Empat Buku Arsitektur) di Venesia. Buku yang dicetak secara luas ini sebagian besar bertanggung jawab menyebarkan gagasan Renaisans di Italia ke seluruh Eropa, yang dibantu dengan karya pendukungnya seperti diplomat Inggris Henry Wotton, yang karyanya diterbitkan tahun 1624 dengan judul The Elements of Architecture.[24] Proporsi setiap ruangan di dalam vila dihitung berdasarkan rasio matematika sederhana seperti 3:4 dan 4:5, dan ruangan yang berbeda di dalam rumah saling terkait dengan rasio ini. Arsitek sebelumnya telah menggunakan formula ini untuk menyeimbangkan satu fasad simetris; namun, desain Palladio berhubungan dengan keseluruhan, yang biasanya berbentuk persegi, seperti vila.[25] Palladio mengizinkan sejumlah rasio dalam Quattro libri , yang menyatakan:[26][27]

Ada tujuh jenis ruangan yang paling indah dan proporsional dan ternyata lebih baik: bentuk-bentuk ini bisa dibuat melingkar, meski hal ini jarang; atau persegi; atau panjangnya akan sama dengan diagonal luas perseginya; atau persegi dan sepertiga; atau satu setengah persegi; atau persegi dan dua pertiga; atau dua persegi.[c]

Pada tahun 1615, Vincenzo Scamozzi menerbitkan risalah Renaisans akhir berjudul L'Idea dell'Architettura Universale (Gagasan Arsitektur Universal).[28] Dia berusaha menghubungkan desain kota dan bangunan dengan gagasan Vitruvius dan Pythagoras, dan gagasan Palladio yang lebih baru.[29]

Abad ke-19

Kisi mercusuar hiperboloid oleh Vladimir Shukhov, Ukraina, tahun 1911.

Struktur hiperboloid mulai digunakan menjelang akhir abad ke-19 oleh Vladimir Shukhov untuk tiang, mercusuar dan menara pendingin. Bentuk mencolok keduanya selain kuat, juga menarik secara estetika, dan menggunakan bahan struktural yang ekonomis. Menara hiperboloidal Shukhov pertama dipamerkan di Nizhny Novgorod pada tahun 1896.[30][31][32]

Abad ke-20

Informasi lebih lanjut: Arsitektur modern
'Slide' De Stijl, bidang yang saling berpotongan: Rumah Rietveld Schröder, tahun 1924.

Gerakan Arsitektur Modern pada awal abad ke-20 dipelopori[e] oleh Konstruktivisme Rusia,[33] yang menggunakan geometri Euklid rectilinear (juga disebut Kartesian). Dalam gerakan De Stijl, bidang horizontal dan vertikal dipandang sebagai sesuatu yang universal. Bentuk arsitekturnya terdiri dari penempatan dua kecenderungan arah secara bersamaan, menggunakan bidang atap, bidang dinding dan balkon, yang meluncur dengan melewati atau saling berpotongan satu sama lain, seperti pada Rumah Rietveld Schröder pada tahun 1924 oleh Gerrit Rietveld.[34]

Gambar bunga poppy dan tempat merica (biomimetik) Raoul Heinrich Francé dari Die Pflanze als Erfinder, tahun 1920.

Arsitek modernis bebas menggunakan kurva dan juga bidang datar. Stasiun Arnos Charles Holden pada tahun 1933 memiliki ruang tiket yang melingkar dari bata dengan atap beton yang datar.[35] Pada tahun 1938, pelukis Bauhaus Laszlo Moholy-Nagy mengadopsi tujuh elemen bioteknik Raoul Heinrich Francé, yaitu bentuk kristal, bola, kerucut, bidang datar, strip (kuboidal), batang (silinder), dan spiral, seperti halnya blok dasar bangunan arsitektur, yang terinspirasi dari alam.[36][37]

Le Corbusier mengusulkan skala antropometrik dari proporsi dalam arsitektur, di mana Modulor didasarkan pada tinggi badan manusia.[38] Karya Le Corbusier pada tahun 1955, yaitu Chapelle Notre Dame du Haut Le Corbusier menggunakan kurva bentuk bebas yang tidak dapat digambarkan dalam formula matematika.[f] Bentuk-bentuk tersebut terinspirasi dari bentuk-bentuk alamiah seperti bentuk jalannya kapal atau bentuk tangan yang sedang berdoa.[41] Desainnya hanya pada skala terbesar: tidak ada hierarki rinci pada skala yang lebih kecil, dan karenanya tidak memiliki dimensi fraktal. Hal yang sama berlaku untuk bangunan pada abad ke-20 yang terkenal lainnya, seperti Gedung Opera Sydney, Bandara Internasional Denver, dan Museum Guggenheim, di Bilbao.[39]

Arsitektur kontemporer, menurut pendapat 90 arsitek terkemuka yang menanggapi Survei Arsitektur Dunia pada tahun 2010, sangat beragam; di mana Museum Guggenheim karya Frank Gehry di Bilbao, dinilai sebagai yang terbaik.[42]

Bangunan akhir Bandara Internasional Denver, yang selesai dibangun tahun 1995, memiliki atap kain yang didukung dengan permukaan minimum (yaitu nilai kelengkungan rata-rata adalah nol) oleh kabel baja. Bangunan ini menimbulkan pegunungan Colorado yang tertutup salju dan tenda-tenda teepee penduduk asli Amerika.[43][44]

Permukaan minimum atap kain Bandara Internasional Denver, selesai pada tahun 1995; berbentuk pegunungan Colorado yang tertutup salju dan tenda teepee penduduk asli Amerika.

Richard Buckminster Fuller adalah arsitek yang terkenal dengan desain struktur kerang tipis yang dikenal sebagai kubah geodesik. Kubah Biosfer Montréal berukuran 61 meter (200 ft); dengan diameter 76 meter (249 ft).[45]

Gedung Opera Sydney memiliki atap dramatis yang terdiri dari kubah putih yang membumbung tinggi, yang mengingatkan pada layar kapal; untuk membuatnya memungkinkan didirikan, maka dibangun dengan menggunakan komponen-komponen terstandar, di mana kubah-kubah tersebut semuanya terdiri dari bagian segitiga dari kerang-kerang berbentuk bulat dengan radius sama. Bangunan ini memiliki kelengkungan yang seragam di segala arah.[46]

Gerakan dekonstruksi di akhir abad ke-20 (Deconstructivism) menciptakan kekacauan yang disengaja dengan apa yang Nikos Salingaros sebut dalam A Theory of Architecture, sebagai 'bentuk-bentuk acak' (random forms),[47] dengan kompleksitas tinggi,[48] yang menggunakan dinding-dinding non-paralel, serta kisi yang dilapisi dan kompleks permukaan dua dimensi, seperti pada Gedung Konser Walt Disney dan Museum Guggenheim Frank Gehry, di Bilbao.[49][50] Hingga abad ke-20, mahasiswa arsitektur diwajibkan untuk memiliki landasan dalam matematika. Salingaros berpendapat bahwa modernisme "yang terlalu sederhana, dan didorong secara politis", yang kemudian menjadi dekonstruktivisme yang "anti-sains", telah efektif memisahkan arsitektur dari matematika. Dia juga percaya bahwa "pembalikan nilai matematis" ini berbahaya, karena "estetika yang menjalar" dari arsitektur non-matematis melatih orang "untuk menolak informasi matematis di lingkungan binaan"; Dia juga berpendapat bahwa hal ini berdampak negatif pada masyarakat.[39]

Prinsip-prinsip agama

Mesir Kuno

Informasi lebih lanjut: Rasio emas § Piramida Mesir
Piramida Mesir Kuno di Giza memiliki proporsi matematis, baik secara kebetulan maupun disengaja.
Basis: rasio sisi miring (b:a) untuk piramida seperti Piramida Khufu yang bisa jadi: 1: φ (segitiga Kepler); 3: 5 (segitiga 3-4-5); atau 1:4/π.

Piramida Mesir Kuno adalah kuburan yang dibangun dengan proporsi yang dipilih dengan hati-hati, di mana hal ini telah banyak diperdebatkan. kemiringan lereng sekitar 51°85', dan rasio tinggi kemiringan mencapai setengah panjang dasarnya yaitu 1,619, kurang dari 1% dari rasio emas. Hal ini merupakan metode perancangan yang menyiratkan penggunaan segitiga Kepler (sudut muka jenjang 51°49').[51][52] Meskipun kemungkinan kemiringan piramida dipilih dari segitiga 3-4-5 (sudut muka jenjang 53°8'), yang dikenal dari Papirus Matematika Rhind (sekitar 1650 -1550 SM); atau dari segitiga dengan rasio dasar terhadap sisi miring 1:4/π (sudut muka jenjang 51°50').[53]

Kemungkinan penggunaan segitiga 3-4-5 yang menghasilkan sudut kanan, seperti bidang dasar piramida, dan pengetahuan teorema Pythagoras yang akan diimplikasikan, telah banyak ditegaskan.[54] Ini adalah konjektur pertama yang ditemukan oleh sejarawan Moritz Cantor pada tahun 1882.[54] Telah diketahui bahwa sudut kanan ditemukan secara akurat di Mesir Kuno;[54] dan para surveyor mereka menggunakan tali pengikat untuk mengukur;[54] Plutarchos mencatatnya dalam Isis dan Osiris (sekitar tahun 100 M) bahwa orang Mesir mengagumi segitiga 3-4-5;[54] dan bahwa Papyrus Berlin 6619 dari Kerajaan Pertengahan Mesir (sebelum tahun 1700 SM) dinyatakan sebagai "luas kuadrat 100 sama dengan dua persegi yang lebih kecil. Satu sisi adalah ½ + ¼ sisi yang lain."[55] Sejarawan matematika Roger L. Cooke mengamati bahwa, "Sulit membayangkan ada orang yang tertarik pada kondisi seperti itu, tanpa mengetahui teorema Pythagoras."[54] Berlawanan dengan pendapat ini, Cooke mencatat bahwa tidak ada teks Mesir sebelum 300 SM yang benar-benar menyebutkan penggunaan teorema untuk menemukan panjang sisi segitiga, dan ada beberapa cara sederhana untuk membangun sudut siku-siku. Cooke menyimpulkan bahwa konjektur Cantor masih tetap tidak pasti: dia juga menduga bahwa orang Mesir Kuno mungkin memang tahu teorema Pythagoras, tapi "tidak ada bukti bahwa mereka menggunakannya untuk membangun sudut kanan".[54]

India kuno

Informasi lebih lanjut: Arsitektur India dan Vastu shastra
Gapura pada Kuil Hindu Virupaksha di Hampi memiliki struktur fraktal, di mana bagian-bagiannya menyerupai keseluruhannya.
Denah Kuil Meenakshi Amman di Madurai, dari abad ke-7 dan seterusnya. Keempat pintu gerbang (nomor I-IV) adalah gapura tinggi.

Vaastu Shastra adalah kanon arsitektur dan perencanaan kota India kuno yang menggunakan gambar simetris yang disebut mandala. Perhitungan kompleks digunakan untuk sampai pada dimensi bangunan dan komponennya. Desainnya dimaksudkan untuk memadukan arsitektur dengan alam, fungsi relatif berbagai bagian struktur, dan kepercayaan kuno menggunakan pola geometris (yantra), simetri dan keteraturan arah.[56][57] Namun, arsitek awal mungkin telah menemukan proporsi matematis dengan tidak sengaja. Ahli matematika Georges Ifrah mencatat bahwa "trik" sederhana dengan tali dan ranting dapat digunakan untuk menyusun bentuk geometri, seperti bentuk elips dan sudut siku-siku.[12][58]

Matematika fraktal telah digunakan untuk menunjukkan alasan mengapa bangunan yang ada memiliki daya tarik universal dan juga memuaskan secara visual; karena pola-pola ini memberikan ketelitian skala dengan jarak pandang yang berbeda. Misalnya, di gerbang-gerbang gapura tinggi kuil Hindu seperti Kuil Virupaksha di Hampi yang dibangun pada abad ke-7, dan yang lainnya seperti Kuil Kandariya Mahadewa di Khajuraho, bagian dan keseluruhannya memiliki karakter yang sama, dengan dimensi fraktal di kisaran 1,7 sampai 1,8. Sekelompok menara kecil (shikhara, lit. 'gunung') tentang menara tertinggi dan berada di tengah; yang mewakili Gunung Kailash yang suci, tempat tinggal Dewa Siwa, menggambarkan pengulangan tak berujung alam semesta dalam kosmologi Hindu.[2][59] Sarjana studi agama William J. Jackson mengamati pola menara yang dikelompokkan di antara menara-menara kecil, dan dikelompokkan di antara menara yang lebih kecil lainnya, bahwa:

Bentuk ideal disulap dengan indah, sehingga menunjukkan tingkat keberadaan dan kesadaran tak terbatas, memperluas ukuran yang menaik menuju transendensi ke atas, dan pada saat yang sama menyimpan tempat suci di dalamnya.[59][60]

Kuil Meenakshi Amman adalah kompleks dengan beberapa tempat suci, di mana jalan-jalan di Madurai terbentang secara konsentris di sekitarnya sesuai yang ditulis dalam shastra. Keempat pintu gerbang menara tinggi (gapura) memiliki struktur fraktal berulang seperti halnya di Hampi. Pagar di sekeliling masing-masing kuil berbentuk persegi panjang, serta dikelilingi tembok-tembok batu yang tinggi.[61]

Yunani kuno

Informasi lebih lanjut: Arsitektur Yunani Kuno, Rasio emas, Pythagoreanisme dan Geometri Euklid
Parthenon dirancang menggunakan rasio Pythagoras.

Pythagoras (sekitar 569 - 475 SM) dan pengikutnya, orang-orang Pythagoras, berpendapat bahwa "segala sesuatu adalah bilangan". Mereka mengamati harmoni yang dihasilkan oleh nada dengan rasio frekuensi bilangan bulat kecil tertentu, dan berpendapat bahwa bangunan juga harus dirancang dengan rasio semacam itu. Kata Yunani 'symmetria' awalnya melambangkan harmoni bentuk arsitektur, dengan rasio yang tepat dari detail terkecil bangunan hingga keseluruhan desainnya.[12]

Denah lantai Parthenon.

Parthenon berdiameter 695 meter (2.280 ft), lebar 309 meter (1.014 ft) dan tinggi 137 meter (449 ft) ke atas cornice (ornamen di atas bangunan atau pilar). Ini memberi rasio lebar dengan panjang 4:9, dan rasio yang sama untuk tinggi dan lebarnya. Menempatkannya bersama-sama memberi nilai tinggi:lebar:panjang 16:36:81[62] dari angka Pythagoras 42:62:92. Nilai-nilai ini menetapkan modul 0,858 m. Persegi panjang dengan rasio 4:9 dapat dibangun dengan tiga persegi panjang, yang bersebelahan pada sisi dalam dengan rasio 3:4. Setiap setengah persegi panjang kemudian merupakan segitiga kanan 3:4:5 yang tepat, yang memungkinkan sudut dan sisi-sisinya dapat diperiksa dengan simpul yang sesuai. Area bagian dalam (naos) memiliki hal yang sama dengan proporsi 4:9 (dengan lebar 2.144 meter (7.034 ft), dan panjang 48,3 m); rasio antara diameter kolom luar, 1.905 meter (6.250 ft), dan jarak pusatnya, 4.293 meter (14.085 ft), yang juga 4:9.[12]

Parthenon dianggap oleh penulis seperti John Julius Norwich sebagai "Kuil Dorik paling sempurna yang pernah ada".[63] Penyempurnaan arsitekturnya yang rumit mencakup "korespondensi halus antara lengkungan stilobat, dinding lancip naos dan entasis kolom".[63] Entasis mengacu pada penurunan subtil diameter kolom saat menaik. Stilobat adalah platform tempat kolom berdiri. Seperti di kuil-kuil Yunani klasik lainnya,[64] platform ini memiliki kelengkungan parabolik kecil mengarah ke atas untuk mengalirkan air hujan dan memperkuat bangunan ketika menahan gempa. Oleh karena itu, kolom itu seharusnya condong ke arah luar, tapi ternyata kolom ini sedikit condong ke dalam sehingga jika terus tegak, kolom-kolom ini akan saling bertemu sekitar satu mil di atas pusat bangunan; karena memiliki ketinggian yang sama, kelengkungan tepi stilobat luar ditransmisikan ke arkitraf dan atap di atas: "semua mengikuti aturan yang dibangun dengan kurva yang rumit".[65]

Rasio emas diketahui pada 300 SM, ketika Euklid menggambarkan metode konstruksi geometris.[66] Telah diketahui bahwa rasio emas digunakan dalam desain Parthenon dan bangunan kuno Yunani lainnya, sama halnya dengan patung, lukisan, dan vas bunga.[67] Penulis terkini seperti Nikos Salingaros, bagaimanapun, meragukan semua klaim ini.[68] Percobaan dengan komputer oleh ilmuwan George Markowsky, gagal menemukan bentuk lain untuk persegi panjang emas.[69]

Arsitektur Islam

Artikel utama: Arsitektur Islam
Court of the Lions, Alhambra memiliki proporsi yang ketat berdasarkan akar kuadrat bilangan bulat kecil.

Sejarawan seni Islam Antonio Fernandez-Puertas mengemukakan bahwa Alhambra, sama seperti Masjid Agung Cordoba,[70] dirancang menggunakan kaki atau 'codo' Hispano-Muslim, sekitar 0,62 meter (2 ft). Di Palace of the Lions (Istana Para Singa), proporsinya mengikuti serangkaian akar dalam matematika. Sebuah persegi panjang dengan sisi 1 dan √2 memiliki nilai (dengan teorema Pythagoras) diagonal √3, yang menggambarkan segitiga siku-siku yang dibuat oleh sisi-sisi bangunan; seri berlanjut dengan √4 (dengan rasio 1: 2), √ 5 dan seterusnya. Pola dekoratif juga berbentuk proporsional, √2 menghasilkan persegi di dalam lingkaran dan bintang bersudut delapan, √3 menghasilkan bintang bersudut enam. Tidak ada bukti yang mendukung klaim sebelumnya bahwa rasio emas digunakan di Alhambra.[10][71] Palace of the Lions dibatasi oleh Aula Dua Suster dan Aula Abelisrajes; bentuk segi enam dapat ditarik dari pusat dua ruangan ini dan keempat sudut di dalam Palace of the Lions.[72]

Masjid Selimiye, tahun 1569-1575.

Masjid Selimiye di Edirne, Turki, dibangun oleh Mimar Sinan yang menyediakan ruang di mana mihrab dapat terlihat dari mana saja di dalam gedung. Ruang pusat yang sangat besar diatur sedemikian rupa sehingga berbentuk segi delapan, yang dibentuk oleh delapan pilar besar, dan dibatasi oleh kubah melingkar berdiameter 31,25 meter (102,5 ft) dan tinggi 43 meter (141 ft). Segi delapan dibentuk menjadi persegi dengan bentuk empat semi-kubah, dan secara eksternal dibangun oleh empat menara yang sangat tinggi, ukuran tingginya 83 meter (272 ft). Denah bangunan tersebut terdiri dari sebuah lingkaran dalam oktagon yang berada dalam persegi.[73]

Arsitektur Mughal

Artikel utama: Arsitektur Mughal, Fatehpur Sikri, dan Asal mula arsitektur Taj Mahal
Mausoleum Taj Mahal dengan bagian taman kompleks di Agra.

Arsitektur Mughal, yang dikenal sebagai peninggalan kota kekaisaran Fatehpur Sikri dan juga kompleks Taj Mahal, memiliki tatanan matematis dan estetika tinggi yang didasarkan pada simetri dan harmoni.[11][74]

Taj Mahal menunjukkan arsitektur Mughal, yang keduanya mewakili surga[75] dan menampilkan kekuasaan Kaisar Mughal, Shah Jahan melalui skala, simetri dan dekorasi mahalnya. Mausoleum dengan marmer putih, dihiasi dengan pietra dura; bangunan-bangunan besar lainnya seperti gerbang besar (Darwaza-i rauza), taman dan jalan secara bersamaan membentuk desain hirarkis terpadu. Bangunan tersebut meliputi sebuah masjid pada batu pasir merah di sebelah barat, dan sebuah bangunan Jawab yang hampir identik, yang secara harfiah berarti 'jawaban' berada di sebelah timur, menjaga simetri bilateral kompleks. Kawasan charbagh (taman empat kali lipat) dengan empat bagian yang melambangkan empat sungai surga, dan menampilkan pemandangan dan pantulan mausoleum; yang dibagi menjadi 16 parter.[76]

Denah lokasi kompleks Taj Mahal. Gerbang besar ada di sebelah kanan, makam di bagian tengahnya, dikelilingi oleh masjid (bawah) dan Jawab. Denahnya meliputi persegi dan oktagon.

Kompleks Taj Mahal diletakkan pada sebuah petak, yang terbagi menjadi petak-petak kecil. Sejarawan arsitektur Koch dan Barraud setuju dengan akun tradisional yang memberi lebar kompleks 374 meter Mughal atau gaz,[g] di mana kawasan utama terbagi menjadi tiga persegi berukuran 374-gaz. Ini terbagi di wilayah seperti bazaar dan perhotelan yang terbagi lagi menjadi ruangan-ruangan berukuran 17-gaz; taman dan teras berada pada luas ruang 23 gaz, dan lebar 368 gaz (16 x 23). Mausoleum, masjid dan pondok tamu ditata di atas petak seluas 7 gaz. Koch dan Barraud mengamati bahwa jika sebuah oktagon digunakan berulang kali dalam sebuah kompleks yang bersisi 7 unit, maka akan memiliki lebar 17 unit,[h] yang akan membantu menjelaskan pilihan nilai rasio pada kompleks.[77]

Arsitektur Kristen

Informasi lebih lanjut: Arsitektur gereja
Hagia Sophia di Istanbul
a) Denah galeri (bagian atas)
b) Denah lantai dasar (bagian bawah).

Basilika patriarkal Kristen Hagia Sophia di Bizantium (sekarang Istanbul), dibangun pertama kali pada tahun 537 (dua kali dibangun ulang), selama seribu tahun[i] adalah katedral terbesar yang pernah didirikan. Hal ini mengilhami banyak bangunan yang didirikan kemudian seperti Sultan Ahmed dan masjid-masjid lain di kota ini. Arsitektur Bizantium mencakup sebuah nave yang dimahkotai oleh kubah bundar dan dua buah kubah-setengah berdiameter sama (31 meter (102 ft)), dengan lima kubah kecil lainnya membentuk apse dan empat sudut bulat dari bagian dalam persegi panjang yang luas.[78] Bentuk ini ditafsirkan oleh arsitek abad pertengahan yang merepresentasikan hal-hal duniawi yang berada di bawah (dasar bujur sangkar) dan langit Ilahiah yang berada di atas (kubah bola yang meninggi).[79] Kaisar Yustinianus I menggunakan dua geometri arsitek Isidorus Miletus dan Anthemius dari Tralles; di mana Isidore menyusun karya Archimedes tentang geometri padat, dan dipengaruhi olehnya.[12][80]

Pentingnya air baptis dalam agama Kristen tercermin dalam skala arsitektur baptisterium. Baptisterium lateran tertua di Roma, dibangun pada tahun 440,[81] menetapkan tren baptisterium oktagonal; di mana bak air pembaptisan di dalam bangunan ini sering kali berbentuk segi delapan, meski baptisterium terbesar berada di Italia, Pisa—yang dibangun antara tahun 1152 dan 1363, berbentuk melingkar, namun bak airnya berbentuk segi delapan. Tingginya 54,86 meter (180 ft), dengan diameter 34,13 meter (112 ft) (nilai rasio 8: 5).[82] Santo Ambrosius menulis bahwa baik air dan baptisterium berbentuk segi delapan "karena ada pada hari ke-8,[j] Dengan kebangkitan Yesus, Kristus melonggarkan ikatan kematian dan menerima orang mati dari kuburan mereka."[83][84] Santo Agustinus juga menggambarkan hari ke-8 sebagai "kekal ... dikuduskan oleh kebangkitan Kristus".[84][85] Baptisterium Saint John yang berbentuk oktagonal, di Firenze yang dibangun antara 1059 dan 1128, adalah salah satu bangunan tertua di kota itu, dan merupakan salah satu bangunan dengan tradisi zaman kuno langsung; hal ini sangat berpengaruh pada Renaisans Firenze berikutnya, dengan arsitek utama seperti Francesco Talenti, Alberti dan Brunelleschi; yang digunakan sebagai model arsitektur klasik.[86]

Nomor lima digunakan 'secara luas'[87] pada tahun 1717 oleh Gereja Ziarah St John dari Nepomuk di Zelená hora, dekat Žďár nad Sázavou di Republik Ceko, yang dirancang oleh Jan Blažej Santini Aichel. Nave tersebut berbentuk melingkar, dikelilingi oleh lima pasang kolom dan lima kubah oval yang bergantian dengan apse ogival. Gereja selanjutnya memiliki lima gerbang, lima kapel, lima altar dan lima bintang; sebuah legenda mengklaim bahwa ketika Santo Yohanes dari Nepomuk menjadi martir, lima bintang muncul di atas kepalanya.[87][88] Arsitektur lima kali lipat juga bisa melambangkan Lima Luka Kudus dan lima huruf dari kata "Tacui" (bahasa Latin: "Saya tetap diam" [tentang rahasia pengakuan dosa]).[89]

Antoni Gaudí menggunakan berbagai struktur geometris, yang beberapa di antaranya adalah permukaan minimum di Sagrada Família, Barcelona, yang mulai dibangun pada tahun 1882 (dan tidak selesai tahun 2015). Struktur ini termasuk bentuk paraboloid hiperbolik dan revolusi hiperboloid,[90] teselasi, kurva katener, katenoid, helikoid, dan permukaan teratur. Perpaduan geometri yang beragam ini dikombinasikan secara kreatif dengan berbagai cara di sekitar gereja. Misalnya, pada Fasad Pasionis Sagrada Família, Gaudí memasang batu yang ber"cabang" dalam bentuk paraboloid hiperbolik, tanpa tumpang tindih di bagian puncaknya (directrices), dan saling bertemu pada satu titik. Sebaliknya, di barisan tiang terdapat permukaan paraboloid hiperbolik yang dengan mulus bergabung dengan struktur lain membentuk permukaan yang tak terbatas. Selanjutnya, Gaudí mengeksplorasi pola alamiah yang matematis pada dirinya sendiri, dengan kolom yang berasal dari bentuk pohon, dan lintel yang terbuat dari basal yang tidak dimodifikasi; namun retak secara alami (akibat pendinginan dari batuan cair) ke dalam kolom heksagonal.[91][92][93]

Katedral Saint Mary of the Assumption di San Francisco yang di bangun tahun 1971, memiliki atap pelana yang terdiri dari delapan segmen paraboloid hiperbolik, yang disusun sedemikian rupa sehingga bagian penampang horizontal paling bawah atap adalah persegi dan bagian paling atasnya adalah salib Kristen. Bangunannya berbentuk persegi dengan sisi 777 meter (2.549 ft), dan tingginya 579 meter (1.900 ft).[94] Katedral Brasília yang dibangun tahun 1970 oleh Oscar Niemeyer menggunakan struktur hiperboloid yang berbeda; yang dibangun dari 16 balok beton identik, masing-masing memiliki berat 90 ton,[k] disusun dalam lingkaran yang membentuk hiperboloid revolusi, balok-balok putih tersebut menciptakan bentuk seperti tangan yang sedang berdoa ke surga. Hanya kubah yang terlihat dari luar, dan sebagian besar bangunan berada di bawah tanah.[95][96][97][98]

Beberapa gereja abad pertengahan di Skandinavia berbentuk melingkar, termasuk empat di pulau Denmark, Bornholm. Østerlars Church 1160 adalah salah satu yang tertua, dan memiliki nave yang melingkar di sekitar batu kolom besar yang melingkar, ditembus dengan lengkungan dan dihiasi dengan lukisan dinding. Struktur melingkar memiliki tiga tingkat dan rupanya diberi benteng, Tingkat paling atas digunakan untuk pertahanan.[99][100]

Dekorasi matematis

Dekorasi arsitektur Islam

Artikel utama: Pola geometri Islam

Bangunan Islam sering dihiasi dengan pola geometris yang biasanya menggunakan beberapa teselasi matematika, yang terbentuk dari keramik (girih, zellige) yang bisa polos atau dihiasi dengan garis-garis.[12] Bentuk simetri bintang enam, delapan, atau kelipatan delapan titik digunakan dalam pola-pola Islam. Beberapa di antaranya didasarkan pada 'Khatem Sulemani' atau motif segel Salomo, yang berbentuk bintang dengan delapan sudut yang terbuat dari dua persegi, satu diputar 45 derajat, dari arah lain di pusat yang sama.[101] Pola-pola Islam banyak dikembangkan dari 17 kemungkinan grup kristalografi. Edith Müller menunjukkan 11 grup kristalografi yang digunakan dalam dekorasi Alhambra di awal tahun 1944, sementara pada tahun 1986, Branko Grünbaum mengklaim telah menemukan 13 grup kristalografi di Alhambra, dengan menyatakan secara kontroversial bahwa 4 kelompok yang tersisa tidak ditemukan di manapun dalam ornamen Islam.[101]

  • Geometri kompleks dan lapisan ubin muqarnas yang berkubah di Masjid Sheikh Lotfollah, Isfahan, 1603–1619.
    Geometri kompleks dan lapisan ubin muqarnas yang berkubah di Masjid Sheikh Lotfollah, Isfahan, 1603–1619.
  • Louvre Abu Dhabi dibangun tahun 2015, kubahnya dibangun dari lapisan bintang oktagon, segitiga, dan persegi.
    Louvre Abu Dhabi dibangun tahun 2015, kubahnya dibangun dari lapisan bintang oktagon, segitiga, dan persegi.

Dekorasi arsitektur modern

Informasi lebih lanjut: Ornamen (arsitektur) dan Arsitektur kontemporer

Menjelang akhir abad ke-20, konstruksi matematika baru seperti geometri fraktal dan ubin aperiodik digunakan oleh arsitek untuk memberikan penutup yang atraktif dan menarik digunakan sebagai ornamen bangunan.[4] Pada tahun 1913, arsitek modernis, Adolf Loos telah menyatakan, "Ornamen adalah sebuah kejahatan",[102] yang mempengaruhi pemikiran arsitektur di akhir abad ke-20. Di abad 21, arsitek kembali mulai mengeksplorasi penggunaan ornamen. Ornamen abad ke 21 sangat beragam. Pusat Konser dan Konferensi Harpa, Henning Larsen, tahun 2011, Reykjavik memiliki dinding batu yang terbuat dari balok kaca besar.[102] Kantor arsitek asing di Ravensbourne College 2010 London, dibuat dengan hiasan teselasi secara dekoratif; dengan 28.000 ubin aluminium yang telah dianodisasi membentuk ubin berwarna merah, putih dan coklat yang saling terkait pada jendela yang melingkar dengan ukuran yang berbeda. Teselasi menggunakan tiga jenis ubin, segitiga sama sisi dan dua pentagon yang tidak beraturan.[103][104][l] Perpustakaan Kanazawa Umimirai milik Kazumi Kudo menciptakan kisi dekoratif yang terbuat dari balok kecil yang melintang, dan terbuat dari kaca yang dipasang di dinding beton polos.[102]

Benteng pertahanan

Eropa

Informasi lebih lanjut: Benteng selekoh

Arsitektur benteng berkembang dari benteng abad pertengahan, yang memiliki dinding batu tinggi, ke benteng bintang simetris rendah; yang mampu menahan pemboman artileri antara pertengahan abad ke-15 dan ke-19. Geometri bentuk bintang didikte atas kebutuhan untuk menghindari zona mati, di mana infanteri yang menyerang dapat berlindung dari senjata api pertahanan; sisi-sisi pada titik-titik yang diproyeksikan miring, memungkinkan api dapat menyapu tanah, dan memberikan baku tembak (dari kedua sisi) dan melampaui setiap titik proyeksi. Arsitek terkenal yang merancang benteng pertahanan tersebut diantaranya adalah Michelangelo, Baldassare Peruzzi, Vincenzo Scamozzi dan Sébastien Le Prestre de Vauban.[105][106]

Sigfried Giedion, seorang sejarawan arsitektur, berpendapat bahwa benteng berbentuk bintang memiliki pengaruh formatif terhadap pola kota ideal Renaisans: "Renaisans telah dihipnosis oleh satu tipe kota yang selama satu setengah abad—dari Filarete hingga Scamozzi—terkesan dengan semua skema utopis, yaitu kota berbentuk bintang."[107]

Tiongkok

Sebuah tulou di Kabupaten Yongding, provinsi Fujian.

Dalam arsitektur Tiongkok, tulou yang berbentuk melingkar, dan berada di provinsi Fujian; memiliki struktur pertahanan komunal dengan dinding kosong dan satu pintu kayu berlapis besi, beberapa berasal dari abad ke-16. Dindingnya ditutup dengan atap yang meluncur perlahan ke arah luar dan ke dalam, membentuk cincin. Bagian tengah lingkaran adalah halaman berbatu terbuka, yang sering kali dikelilingi oleh galeri kayu setinggi lima tingkat.[108]

Tujuan lingkungan

Yakhchal di Yazd, Iran.

Arsitek juga dapat memilih bentuk bangunan untuk memenuhi tujuan lingkungan.[87] Misalnya, Foster and Partners '30 St Mary Axe, London, yang dikenal sebagai "The Gherkin"yang berbentuk seperti mentimun, merupakan sebuah revolusi padat yang dirancang dengan menggunakan pemodelan parametrik. Geometrinya dipilih bukan semata-mata untuk alasan estetika, tapi untuk meminimalkan arus udara yang berputar pada bagian dasarnya. Meskipun permukaan bangunannya melengkung, semua panel kaca yang membentuk kulitnya berbentuk rata, kecuali lensa di bagian atas. Sebagian besar panel berbentuk segiempat, karena dapat dipotong dari kaca segi empat, sehingga meminimalisir pemborosan daripada panel segitiga.[1]

Yakhchal tradisional (lubang es) di Persia berfungsi sebagai pendingin evaporatif; yang berada di atas tanah, dengan struktur berbentuk kubah, namun memiliki tempat penyimpanan es dan terkadang juga makanan di bawah tanahnya. Ruang bawah tanah, serta konstruksi tahan panas tebal dapat mengisolasi ruang penyimpanan sepanjang tahun. Ruang bagian dalam sering didinginkan lebih lanjut dengan windcatcher. Es tersedia di musim panas untuk membuat faloodeh atau makanan penutup beku.[109]

Lihat pula

Catatan

  1. ^ Pada Buku 4, bab 3 dari De architectura, dia membahas secara langsung mengenai modulus ini.[15]
  2. ^ Satu kaki Romawi sekitar 0,296 meter (971 ft).
  3. ^ Pada notasi aljabar modern, masing-masing rasio-rasio ini adalah 1:1, √2:1, 4:3, 3:2, 5:3, dan 2:1.
  4. ^ In modern algebraic notation, these ratios are respectively 1:1, √2:1, 4:3, 3:2, 5:3, 2:1.
  5. ^ Sebagai contoh, konstruktivisme banyak dipengaruhi oleh Bauhaus dan Le Corbusier.[33]
  6. ^ Pace Nikos Salingaros berpendapat berlawanan,[39] tetapi tidak jelas matematika seperti apa yang bisa diwujudkan dalam kurva gereja Le Corbusier.[40]
  7. ^ Satu gaz sekitar 0,86 meter (2,8 ft).
  8. ^ Sebuah persegi yang ditarik mengelilingi oktagon dengan memperpanjang sisi-sisinya akan menghasilkan empat segitiga bersudut kanan dengan sisi miring bernilai 7 dan dua sisi lainnya berukuran √(49/2) atau 4.9497 ..., mendekati 5. Sisi persegi tersebut adalah 5 + 7 + 5, sama dengan 17.
  9. ^ Hingga Katedral Sevilla selesai dibangun pada tahun 1520.
  10. ^ Hari keenam Pekan suci adalah Jumat Agung; yaitu hari Minggu (dari kebangkitan) yang merupakan hari ke-8.[83]
  11. ^ Yaitu 90 ton (89 ton panjang; 99 ton pendek).
  12. ^ Sebuah ubin aperiodik telah dipertimbangkan, untuk menghindari ritme grid struktural, namun dalam prakteknya ubin Penrose terlalu rumit, sehingga grid 2.625m dipilih di bagian horizontal dan 4.55m di bagian vertikal.[104]

Referensi

  1. ^ a b c Freiberger, Marianne (1 March 2007). "Perfect buildings: the maths of modern architecture". Plus magazine. Diarsipkan dari versi asli tanggal 2015-04-23. Diakses tanggal 5 October 2015. 
  2. ^ a b Rian, Iasef Md; Park, Jin-Ho; Ahn, Hyung Uk; Chang, Dongkuk (2007). "Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho". Building and Environment. 42: 4093–4107. doi:10.1016/j.buildenv.2007.01.028. Diarsipkan dari versi asli tanggal 2016-03-31. Diakses tanggal 2017-11-23. 
  3. ^ Williams, Kim; Ostwald, Michael J., ed. (2015). Architecture and Mathematics from Antiquity to the Future: Volume I: from Antiquity to the 1500s. Birkhäuser. hlm. chapter 1. 1–24. ISBN 978-3-319-00136-4. 
  4. ^ a b Williams, Kim; Ostwald, Michael J., ed. (2015). Architecture and Mathematics from Antiquity to the Future: Volume II: The 1500s to the Future. Birkhäuser. hlm. chapter 48. 1–24. ISBN 978-3-319-00142-5. 
  5. ^ "Architectural Engineering Overview" (PDF). Sloan Career Cornerstone Center. Diarsipkan dari versi asli (PDF) tanggal 2015-07-14. Diakses tanggal 11 October 2015. 
  6. ^ Leyton, Michael (2001). A Generative Theory of Shape. Springer. ISBN 978-3-540-42717-9. 
  7. ^ Stakhov, Alexey; Olsen, Olsen (2009). The Mathematics of Harmony: From Euclid to Contemporary Mathematics and Computer Science. World Scientific. ISBN 978-981-277-582-5. 
  8. ^ Smith, William (1870). Dictionary of Greek and Roman Biography and Mythology. Little, Brown. hlm. 620. 
  9. ^ a b Vitruvius (2009). On Architecture. Penguin Books. hlm. 8–9. ISBN 978-0-14-193195-1. 
  10. ^ a b Tennant, Raymond (July 2003). "International Joint Conference of ISAMA, the International Society of the Arts, Mathematics, and Architecture, and BRIDGES. Mathematical Connections in Art Music, and Science, University of Granada, Spain, July, 2003. Islamic Constructions: The Geometry Needed by Craftsmen" (PDF). International Joint Conference of ISAMA, the International Society of the Arts, Mathematics, and Architecture, and BRIDGES, Mathematical Connections in Art Music, and Science. Diarsipkan (PDF) dari versi asli tanggal 2015-12-24. Diakses tanggal 2017-11-23. 
  11. ^ a b Rai, Jaswant (1993). "Mathematics and Aesthetics in Islamic Architecture: Reference to Fatehpur Sikri". Journal of King Saud University, Architecture & Planning. 5 (1): 19–48. [pranala nonaktif permanen]
  12. ^ a b c d e f O'Connor, J. J.; Robertson, E. F. (February 2002). "Mathematics and Architecture". University of St Andrews. Diarsipkan dari versi asli tanggal 2015-10-13. Diakses tanggal 4 October 2015. 
  13. ^ van den Hoeven, Saskia; van der Veen, Maartje (2010). "Muqarnas: Mathematics in Islamic Arts" (PDF). Utrecht University. Diarsipkan dari versi asli (PDF) tanggal 2016-03-04. Diakses tanggal 30 September 2015. 
  14. ^ Cucker, Felipe (2013). Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. Cambridge University Press. hlm. 103–106. ISBN 978-0-521-72876-8. 
  15. ^ Vitruvius. "VITRUVIUS, BOOK IV, CHAPTER 3 On the Doric order". Vitruvius.be. Diarsipkan dari versi asli tanggal 2016-03-04. Diakses tanggal 6 October 2015. 
  16. ^ Williams, Kim; Ostwald, Michael J. (9 February 2015). Architecture and Mathematics from Antiquity to the Future: Volume I: Antiquity to the 1500s. Birkhäuser. hlm. 42, 48. ISBN 978-3-319-00137-1. 
  17. ^ Roth, Leland M. (1992). Understanding Architecture: Its Elements, History, And Meaning. Boulder: Westview Press. hlm. 36. ISBN 0-06-438493-4. 
  18. ^ Claridge, Amanda (1998). Rome. Oxford Archaeological Guides. Oxford Oxfordshire: Oxford University Press. hlm. 204–5. ISBN 0-19-288003-9. 
  19. ^ Lancaster, Lynne C. (2005). Concrete Vaulted Construction in Imperial Rome: Innovations in Context. Cambridge: Cambridge University Press. hlm. 44–46. ISBN 0-521-84202-6. 
  20. ^ Typ 525.69.781, Houghton Library, Harvard University
  21. ^ March, Lionel (1996). "Renaissance mathematics and architectural proportion in Alberti's De re aedificatoria". Architectural Research Quarterly. 2 (1): 54–65. doi:10.1017/S135913550000110X. 
  22. ^ "Sphere circumscribing a cube". Mathalino.com Engineering Math Review. Diarsipkan dari versi asli tanggal 2015-09-22. Diakses tanggal 4 October 2015. 
  23. ^ Andersen, Kirsti (2008). The Geometry of an Art: The History of the Mathematical Theory of Perspective from Alberti to Monge. Springer. hlm. 117–121. ISBN 978-0-387-48946-9. 
  24. ^ Ruhl, Carsten (7 April 2011). "Palladianism: From the Italian Villa to International Architecture". European History Online. Diarsipkan dari versi asli tanggal 2015-10-04. Diakses tanggal 3 October 2015. 
  25. ^ Copplestone, Trewin (1963). World Architecture. Hamlyn. hlm. 251. 
  26. ^ Wassell, Stephen R. "The Mathematics Of Palladio's Villas: Workshop '98". Nexus Network Journal. Diarsipkan dari versi asli tanggal 2015-12-18. Diakses tanggal 3 October 2015. 
  27. ^ Palladio, Andrea; Tavernor, Robert; Schofield, Richard (trans.) (1997) [1570]. I quattro libri dell'architettura. MIT Press. hlm. book I, chapter xxi, page 57. 
  28. ^ Scamozzi, Vincenzo; Vroom, W. H. M. (trans.) (2003) [1615]. The Idea of a Universal Architecture. Architectura & Natura. 
  29. ^ Borys, Ann Marie (28 March 2014). Vincenzo Scamozzi and the Chorography of Early Modern Architecture. Ashgate Publishing. hlm. 140–148 and passim. ISBN 978-1-4094-5580-6. 
  30. ^ Beckh, Matthias (2015). Hyperbolic Structures: Shukhov's Lattice Towers - Forerunners of Modern Lightweight Construction. John Wiley & Sons. hlm. 75 and passim. ISBN 978-1-118-93268-1. 
  31. ^ "The Nijni-Novgorod exhibition: Water tower, room under construction, springing of 91 feet span". The Engineer: 292–294. 19 March 1897. 
  32. ^ Graefe, Rainer; et al. (1990). Vladimir G. Suchov 1853—1939. Die Kunst der sparsamen Konstruktion. Deutsche Verlags-Anstalt. hlm. 110–114. ISBN 3-421-02984-9. 
  33. ^ a b Hatherley, Owen (4 November 2011). "The Constructivists and the Russian Revolution in Art and Architecture". The Guardian. Diarsipkan dari versi asli tanggal 2018-01-03. Diakses tanggal 6 June 2016. 
  34. ^ "Rietveld Schröderhuis (Rietveld Schröder House)". World Heritage Centre. UNESCO. Diarsipkan dari versi asli tanggal 2017-07-11. Diakses tanggal 13 December 2012. 
  35. ^ Historic England. "Details from listed building database (1358981)". Daftar Warisan Nasional Inggris. Diakses tanggal 5 October 2015. 
  36. ^ Moholy-Nagy, Laszlo; Hoffman, Daphne M. (trans.) (1938). The New Vision: Fundamentals of Design, Painting, Sculpture, Architecture. New Bauhaus Books. hlm. 46. 
  37. ^ Gamwell, Lynn (2015). Mathematics and Art: A Cultural History. Princeton University Press. hlm. 306. ISBN 978-0-691-16528-8. 
  38. ^ Le Corbusier (2004) [1954 and 1958]. The Modulor: A Harmonious Measure to the Human Scale, Universally Applicable to Architecture and Mechanics. Birkhäuser. ISBN 3-7643-6188-3. 
  39. ^ a b c Salingaros, Nikos. "Architecture, Patterns, and Mathematics". Nexus Network Journal. Diarsipkan dari versi asli tanggal 2016-03-03. Diakses tanggal 9 October 2015.  Updated version of Salingaros, Nikos (April 1999). "Architecture, Patterns, and Mathematics". Nexus Network Journal. 1 (2). 
  40. ^ Greene, Herb. "Le Corbusier: Notre Dame du Haut at Ronchamp". Diarsipkan dari versi asli tanggal 2015-09-07. Diakses tanggal 5 October 2015. 
  41. ^ Hanser, David A. (2006). Architecture of France. Greenwood Publishing Group. hlm. 211. ISBN 978-0-313-31902-0. 
  42. ^ "Vanity Fair's World Architecture Survey: the Complete Results". Vanity Fair. 30 June 2010. Diarsipkan dari versi asli tanggal 2014-11-08. Diakses tanggal 22 July 2010. 
  43. ^ "Denver International Airport Press Kit" (PDF). Denver International Airport. 2014. Diarsipkan dari versi asli (PDF) tanggal 12 April 2015. Diakses tanggal 5 October 2015. 
  44. ^ "Denver International Airport". Fenstress Architects. Diarsipkan dari versi asli tanggal 2015-10-06. Diakses tanggal 5 October 2015. 
  45. ^ "Biosphere". A view on cities. Diarsipkan dari versi asli tanggal 2007-09-27. Diakses tanggal 1 October 2015. 
  46. ^ Hahn, Alexander J. (4 February 2013). "Mathematical Excursions To Architecture". Inside Science. Diarsipkan dari versi asli tanggal 2015-10-08. Diakses tanggal 5 October 2015. 
  47. ^ Salingaros, Nikos (2006). A Theory of Architecture. Umbau. hlm. 139–141. 
  48. ^ Salingaros, Nikos (2006). A Theory of Architecture. Umbau. hlm. 124–125. 
  49. ^ Gehry, Frank O.; Mudford, Grant; Koshalek, Richard (2009). Symphony: Frank Gehry's Walt Disney Concert Hall. Five Ties. 
  50. ^ Garcetti, Gil (2004). Iron: Erecting the Walt Disney Concert Hall. Princeton Architectural Press. 
  51. ^ Markowsky, George (January 1992). "Misconceptions About the Golden Ratio" (PDF). The College Mathematics Journal. 23 (1). Diarsipkan (PDF) dari versi asli tanggal 2008-04-08. Diakses tanggal 2017-11-23. 
  52. ^ Taseos, Socrates G. (1990). Back in Time 3104 B.C. to the Great Pyramid. SOC Publishers. 
  53. ^ Gazale, Midhat (1999). Gnomon: From Pharaohs to Fractals. Princeton University Press. 
  54. ^ a b c d e f g Cooke, Roger L. (2011). The History of Mathematics: A Brief Course (edisi ke-2nd). John Wiley & Sons. hlm. 237–238. ISBN 978-1-118-03024-0. 
  55. ^ Gillings, Richard J. (1982). Mathematics in the Time of the Pharaohs. Dover. hlm. 161. 
  56. ^ Kramrisch, Stella (1976), The Hindu Temple Volume 1 & 2, ISBN 81-208-0223-3
  57. ^ Vibhuti Sachdev, Giles Tillotson (2004). Building Jaipur: The Making of an Indian City. hlm. 155–160. ISBN 978-1-86189-137-2. 
  58. ^ Ifrah, Georges (1998). A Universal History of Numbers. Penguin. 
  59. ^ a b c "Fractals in Indian Architecture". Yale University. Diarsipkan dari versi asli tanggal 2012-02-06. Diakses tanggal 1 October 2015. 
  60. ^ Jackson, William J. "For All Fractal Purposes ... an introduction". Indiana University-Purdue University Indianapolis. Diarsipkan dari versi asli tanggal 14 September 2015. Diakses tanggal 1 October 2015. 
  61. ^ King, Anthony D. (2005). Buildings and Society: Essays on the Social Development of the Built Environment. Taylor & Francis. hlm. 72. ISBN 0-203-48075-9. 
  62. ^ Maor, Eli (2007). The Pythagorean Theorem: A 4,000-year History. Princeton University Press. hlm. 19. ISBN 0-691-12526-0. 
  63. ^ a b Norwich, John Julius (2001). Great Architecture of the World. Artists House. hlm. 63. 
  64. ^ Penrose, Francis (1973) [1851]. Principles of Athenian Architecture. Society of Dilettanti. hlm. ch. II.3, plate 9. 
  65. ^ Stevens, Gorham P. (July 1962). "Concerning the Impressiveness of the Parthenon". American Journal of Archaeology. 66 (3): 337–338. doi:10.2307/501468. 
  66. ^ Euclid. Elements. Book 6, Proposition 30.
  67. ^ Archibald, R. C. "Notes on the Logarithmic Spiral, Golden Section and the Fibonacci Series". Diarsipkan dari versi asli tanggal 2015-05-03. Diakses tanggal 1 October 2015. 
  68. ^ Applications of the Golden Mean to Architecture Diarsipkan 2016-03-04 di Wayback Machine.
  69. ^ Markowsky, George (January 1992). "Misconceptions about the Golden Ratio" (PDF). The College Mathematics Journal. 23 (1). Diarsipkan (PDF) dari versi asli tanggal 2008-04-08. Diakses tanggal 2017-11-23. 
  70. ^ Gedal, Najib. "The Great Mosque of Cordoba: Geometric Analysis". Islamic Art & Architecture. Diarsipkan dari versi asli tanggal 2015-10-02. Diakses tanggal 16 October 2015. 
  71. ^ Irwin, Robert (26 May 2011). The Alhambra. Profile Books. hlm. 109–112. ISBN 1-84765-098-8. 
  72. ^ Robertson, Ann (2007). "Revisiting the Geometry of the Sala de Dos Hermanas" (PDF). BRIDGES. Diarsipkan (PDF) dari versi asli tanggal 2015-12-24. Diakses tanggal 11 October 2015. 
  73. ^ Blair, Sheila; Bloom, Jonathan M. (1995). The Art and Architecture of Islam 1250-1800. Yale University Press. ISBN 0-300-06465-9. 
  74. ^ Michell, George; Pasricha, Amit (2011). Mughal Architecture & Gardens. Antique Collectors Club. ISBN 978-1-85149-670-9. 
  75. ^ Parker, Philip (2010). World History. Dorling Kindersley. hlm. 224. ISBN 978-1-4053-4124-0. 
  76. ^ Koch, Ebba (2006). The Complete Taj Mahal: And the Riverfront Gardens of Agra (edisi ke-1st). Thames & Hudson. hlm. 24 and passim. ISBN 0-500-34209-1. 
  77. ^ Koch, Ebba (2006). The Complete Taj Mahal: And the Riverfront Gardens of Agra (edisi ke-1st). Thames & Hudson. hlm. 104–109. ISBN 0-500-34209-1. 
  78. ^ Fazio, Michael; Moffett, Marian; Wodehouse, Lawrence (2009). Buildings Across Time (edisi ke-3rd). McGraw-Hill Higher Education. ISBN 978-0-07-305304-2. 
  79. ^ Gamwell, Lynn (2015). Mathematics and Art: A Cultural History. Princeton University Press. hlm. 48. ISBN 978-0-691-16528-8. 
  80. ^ Kleiner, Fred S.; Mamiya, Christin J. (2008). Gardner's Art Through the Ages: Volume I, Chapters 1–18 (edisi ke-12th). Wadsworth. hlm. 329. ISBN 0-495-46740-5. 
  81. ^ Menander, Hanna; Brandt, Olof; Appetechia, Agostina; Thorén, Håkan (2010). "The Lateran Baptistery in Three Dimensions" (PDF). Swedish National Heritage Board. Diarsipkan dari versi asli (PDF) tanggal 2017-05-16. Diakses tanggal 30 October 2015. 
  82. ^ "The Baptistery". The Leaning Tower of Pisa. Diarsipkan dari versi asli tanggal 2015-10-11. Diakses tanggal 30 October 2015. 
  83. ^ a b Huyser-Konig, Joan. "Theological Reasons for Baptistry Shapes". Calvin Institute of Christian Worship. Diarsipkan dari versi asli tanggal 2015-10-31. Diakses tanggal 30 October 2015. 
  84. ^ a b Kuehn, Regina (1992). A Place for Baptism. Liturgy Training Publications. hlm. 53–60. ISBN 978-0-929650-00-5. 
  85. ^ Augustine of Hippo (426). The City of God. hlm. Book 22, Chapter 30. 
  86. ^ Kleiner, Fred (2012). Gardner's Art through the Ages: A Global History. Cengage Learning. hlm. 355–356. ISBN 1-133-71116-2. 
  87. ^ a b c Simitch, Andrea; Warke, Val (2014). The Language of Architecture: 26 Principles Every Architect Should Know. Rockport Publishers. hlm. 191. ISBN 978-1-62788-048-0. 
  88. ^ "Zelená hora near Žďár nad Sázavou". Czech Tourism. Diarsipkan dari versi asli tanggal 2015-09-06. Diakses tanggal 10 November 2015. 
  89. ^ "Attributes of Saint John of Nepomuk". Saint John of Nepomuk. Diarsipkan dari versi asli tanggal 2016-03-04. Diakses tanggal 10 November 2015. 
  90. ^ Burry, M.C., J.R. Burry, G.M. Dunlop and A. Maher (2001). "Drawing Together Euclidean and Topological Threads (pdf)" (PDF). Presented at SIRC 2001–the Thirteenth Annual Colloquium of the Spatial Information Research Center. Dunedin, New Zealand: University of Otago. Diarsipkan dari versi asli (PDF) tanggal 2007-10-31. Diakses tanggal 2007-11-28. 
  91. ^ "The Geometry of Antoni Gaudi". Math & the Art of MC Escher. Saint Louis University Mathematics and Computer Science. Diarsipkan dari versi asli tanggal 2015-10-07. Diakses tanggal 4 October 2015. 
  92. ^ Usvat, Liliana. "Antony Gaudi and Mathematics". Mathematics Magazine. Diarsipkan dari versi asli tanggal 2015-09-14. Diakses tanggal 4 October 2015. 
  93. ^ M.C. Burry; J.R. Burry; G.M. Dunlop; A. Maher (2001). "Drawing Together Euclidean and Topological Threads" (PDF). The 13th Annual Colloquium of the Spatial Information Research Centre, University of Otago, Dunedin, New Zealand. Diarsipkan dari versi asli (PDF) tanggal 25 June 2008. Diakses tanggal 5 August 2008. 
  94. ^ Nervi, Pier Luigi. "Cathedral of Saint Mary of the Assumption". Architectuul. Diarsipkan dari versi asli tanggal 2015-10-12. Diakses tanggal 12 October 2015. 
  95. ^ "Brasilia Cathedral". About Brasilia. Diarsipkan dari versi asli tanggal 2012-10-30. Diakses tanggal 13 November 2015. 
  96. ^ Behrends, Ehrhard; Crato, Nuno; Rodrigues, Jose Francisco (2012). Raising Public Awareness of Mathematics. Springer Science & Business Media. hlm. 143. ISBN 978-3-642-25710-0. 
  97. ^ Emmer, Michele (2012). Imagine Math: Between Culture and Mathematics. Springer Science & Business Media. hlm. 111. ISBN 978-88-470-2427-4. 
  98. ^ Mkrtchyan, Ruzanna (2013). "Cathedral of Brasilia". Building.AM. Diarsipkan dari versi asli tanggal 2015-11-17. Diakses tanggal 13 November 2015. 
  99. ^ "Østerlars kirke" (dalam bahasa Danish). Nordens kirker. Diarsipkan dari versi asli tanggal 2016-04-02. Diakses tanggal 2 December 2016. 
  100. ^ "Østerlars kirke" (dalam bahasa Danish). Natur Bornholm. Diarsipkan dari versi asli tanggal 2011-07-19. Diakses tanggal 2 December 2016. 
  101. ^ a b Rønning, Frode. "Islamic Patterns And Symmetry Groups" (PDF). University of Exeter. Diarsipkan (PDF) dari versi asli tanggal 2014-01-24. Diakses tanggal 18 April 2014. 
  102. ^ a b c Gibberd, Matt; Hill, Albert (20 August 2013). "The Return of Ornamentation". The Telegraph. Diarsipkan dari versi asli tanggal 2015-09-11. Diakses tanggal 12 October 2015. 
  103. ^ "Ravensbourne College by Foreign Office Architects". de zeen magazine. 13 September 2010. Diarsipkan dari versi asli tanggal 2015-09-24. Diakses tanggal 12 October 2015. 
  104. ^ a b Bizley, Graham. "FOA's peninsula patterns for Ravensbourne College". bdonline.co.uk. Diarsipkan dari versi asli tanggal 2015-09-15. Diakses tanggal 16 October 2015. 
  105. ^ Duffy, C. (1975). Fire & Stone, The Science of Fortress Warfare 1660–1860. Booksales. ISBN 978-0-7858-2109-0. 
  106. ^ Chandler, David (1990). The Art of Warfare in the Age of Marlborough. Spellmount. ISBN 978-0-946771-42-4. 
  107. ^ Giedion, Siegfried (1962) [1941]. Space, Time and Architecture. Harvard University Press. hlm. 43. 
  108. ^ O'Neill, Tom (4 January 2015). "China's Remote Fortresses Lose Residents, Gain Tourists". National Geographic (majalah). Diarsipkan dari versi asli tanggal 2017-10-03. Diakses tanggal 6 January 2017. 
  109. ^ Mahdavinejad, M.; Javanrudi, Kavan (July 2012). "Assessment of Ancient Fridges: A Sustainable Method to Storage Ice in Hot-Arid Climates". Asian Culture and History. 4 (2). doi:10.5539/ach.v4n2p133. 

Pranala luar
Kembali kehalaman sebelumnya