Sage
Анимированный график, созданный в Sage, y=x2 (красная кривая), y=x3(синяя кривая)
Тип	Система компьютерной алгебры
Разработчик	Стейн, Уильям Артур[вд]
Написана на	Python, Cython
Операционная система	Кроссплатформенное программное обеспечение
Первый выпуск	24 февраля 2005
Аппаратная платформа	Python
Последняя версия	10.5 (4 декабря 2024)[1]
Репозиторий	github.com/sagemath/sage
Лицензия	GNU General Public License
Сайт	sagemath.org
Медиафайлы на Викискладе

Sage (с англ. — «мудрец») — система компьютерной алгебры, покрывающая много областей математики, включая алгебру, комбинаторику, вычислительную математику и матанализ.

Первая версия Sage была выпущена 24 февраля 2005 года в виде свободного программного обеспечения с лицензией GNU GPL. Первоначальной целью проекта было «создание открытого программного обеспечения альтернативного системам Magma, Maple, Mathematica, и MATLAB»^[2]. Основной разработчик — математик Вашингтонского университета Уильям Стейн.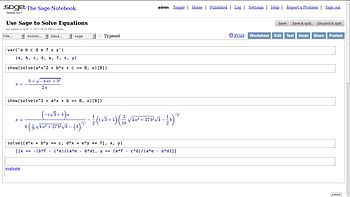

Основной интерфейс системы — интерактивный блокнот, обеспечивающий просмотр и повторное использование введённых команд, вывод и сохранение полученных результатов, включая графики и текстовые аннотации, доступный из большинства современных веб-браузеров. Поддерживается защищённое соединение через протокол HTTPS. Может выполняться как локально, так и удалённо.

Есть интерфейс ввода на основе командной строки с использованием языка Python (начиная с Sage версии 9.0 — Python версии 3, ранее — Python версии 2).

Поддерживаются параллельные вычисления с использованием как многоядерных процессоров, многопроцессорных систем, так и систем распределённых вычислений.

Матанализ реализован на основе систем Maxima и SymPy. Линейная алгебра реализована на основе систем GSL, SciPy и NumPy. Реализованы собственные библиотеки элементарных и специальных математических функций. Есть средства работы с матрицами и массивами данных с поддержкой разреженных массивов. Имеются различные статистические библиотеки функций, использующие функциональность R и SciPy.

Функции и данные можно выводить в виде плоских и трёхмерных графиков. Есть набор инструментов для добавления собственного пользовательского интерфейса к вычислениям и приложениям^[3]. Имеются средства подготовки научно-технической документации с использованием редактора формул и возможностью встраивания Sage в документацию формата LaTeX^[4].

Поддерживается импорт и экспорт различных форматов данных: изображений, видео, аудио, САПР, ГИС, документов и медицинских форматов. Для обработки изображений используются pylab и Python; имеются средства теоретико-графового анализа и визуализации графов.

Есть возможность соединения с базами данных. Поддерживаются различные сетевые протоколы, включая HTTP, NNTP, IMAP, SSH, IRC, FTP.

Реализованы программные интерфейсы для работы с системами Mathematica (также Sage может быть вызван из интерфейса Mathematica^[5][6]), Magma и Maple.

Исходный код и исполняемые файлы Sage доступны для скачивания. При сборке системы многие входящие в комплект библиотеки будут автоматически настроены для оптимальной работы на данном оборудовании, принимая в расчёт количество процессоров и ядер, размер кэш-буферов и поддержку специальных наборов инструкций, например SSE.

В процессе разработки Sage Уильям Стейн основывался на том, что для создания достойной альтернативы системам Magma, Maple, Mathematica, и MATLAB потребуются сотни или тысячи человеко-лет, если начинать процесс разработки с нуля, при этом существует большое количество готового математического программного обеспечения с открытым исходным кодом, но написанного на различных языках программирования, из которых наиболее встречаемыми являются Си, C++, Фортран и Python.

Таким образом, вместо того, чтобы начинать с нуля, было решено объединить всё специализированное математическое программное обеспечение в систему с общим интерфейсом. Конечному пользователю необходимо лишь знать язык Python. Если для какой-то частной задачи не существовало программного обеспечения с открытым кодом, тогда стояла задача написания соответствующего блока для Sage, при этом, в отличие от коммерческих систем компьютерной алгебры, часто использовались исходные коды уже имеющегося свободного программного обеспечения.

К разработке Sage привлекаются как профессионалы, так и студенты. Разработчики работают на общественных началах и поддерживаются грантами^[7].

Sage — свободное программное обеспечение, распространяемое по условиям лицензии GNU General Public License версии 2+. Исходный код может быть скачан с официального сайта. Также доступны выпуски, находящиеся в процессе разработки, хотя они не рекомендуются обычным пользователям. Исполняемые файлы доступны для операционных систем Linux, Windows, OS X и Solaris (как под архитектуру x86, так и SPARC). Также доступен live CD с версией Linux, что позволяет опробовать Sage без установки на компьютер.

Пользователи могут использовать онлайн-версию Sage. При этом имеются ограничения на объём доступной памяти и конфиденциальность работы.

В 2007 году Sage выиграл первый приз международного конкурса свободного программного обеспечения Les Trophées du Libre^[англ.] в разделе научного программного обеспечения^[8].

x,a,b,c = var('x,a,b,c')

log(sqrt(a)).simplify_log() # returns (log(a))/2
log(a/b).simplify_log() # returns log(a) - log(b)
sin(a+b).simplify_trig() # returns cos(a)*sin(b) + sin(a)*cos(b)
cos(a+b).simplify_trig() # returns cos(a)*cos(b) - sin(a)*sin(b)
(a+b)^5 # returns (b + a)^5
expand((a+b)^5) # returns b^5 + 5*a*b^4 + 10*a^2*b^3 +
 # 10*a^3*b^2 + 5*a^4*b + a^5

limit((x^2+1)/(2+x+3*x^2), x=infinity) # returns 1/3
limit(sin(x)/x, x=0) # returns 1

diff(acos(x),x) # returns -1/sqrt(1 - x^2)
f = exp(x)*log(x)
f.diff(x,3) # returns e^x*log(x) + 3*e^x/x - 3*e^x/x^2 + 2*e^x/x^3

solve(a*x^2 + b*x + c, x) # returns [x == (-sqrt(b^2 - 4*a*c) - b)/(2*a),
 # x == (sqrt(b^2 - 4*a*c) - b)/(2*a)]

f = x^2 + 432/x
solve(f.diff(x)==0,x) # returns [x == 3*sqrt(3)*I - 3,
 # x == -3*sqrt(3)*I - 3, x == 6]

t = var('t') # define a variable t
x = function('x',t) # define x to be a function of that variable
DE = lambda y: diff(y,t) + y - 1
desolve(DE(x(t)), [x,t]) # returns '%e^-t*(%e^t+%c)'

A = Matrix([[1,2,3],[3,2,1],[1,1,1]])
y = vector([0,-4,-1])
A.solve_right(y) # returns (-2, 1, 0)
A.eigenvalues() # returns [5, 0, -1]

B = Matrix([[1,2,3],[3,2,1],[1,2,1]])
B.inverse()
# [ 0 1/2 -1/2]
# [-1/4 -1/4 1]
# [ 1/2 0 -1/2]

# Moore-Penrose pseudo-inverse
C = Matrix([[1 , 1], [2 , 2]])
C.pseudoinverse()
# [1/10  1/5]
# [1/10  1/5]

prime_pi(1000000) # returns 78498, the number of primes less than one million

E = EllipticCurve('389a') # construct an elliptic curve from its Cremona label
P, Q = E.gens()
7*P + Q # returns (2869/676 : -171989/17576 : 1)

Построение в Sage лемнискаты Жероно, используя неявно заданную функцию.

Лемниската Жероно — плоская кривая, удовлетворяющая уравнению ${\displaystyle \textstyle x^{4}=a^{2}(x^{2}-y^{2})}$.

## Лемниската Жероно
## x^4=a^2*(x^2-y^2)

a=1
var('x y')
pl=implicit_plot(x^4-(a^2)*(x^2-y^2), (x,-a,a), (y,-a,a),linewidth=2, gridlines=True,frame=False,axes=True)
pl.show()

Основные выпуски:

	Имеется викиучебник по теме «Sage (на английском языке)»

• Project home page (англ.)
• Free software brings affordability, transparency to mathematics (англ.)
• AMS Notices Opinion — Open Source Mathematical Software (англ.)
• Таранчук В. Б. Основные функции систем компьютерной алгебры (рус.). — Минск: БГУ, 2013. — 59 p.