برنامه‌ریزی حرکت (نام دیگر، «مشکل ناوبری»، مسئله «حرکت دهنده پیانو») اصطلاحی است که در رباتیک به فرایند جزئی‌سازی کاری، درقالب حرکت‌های جداگانه و گسسته گفته می‌شود. به عنوان مثال، هدایت رباتی سیار در داخل یک ساختمان به سمت هدفی دور را، در حالی که باید از دیوارها بدون برخورد عبور کند و مراقب پایین افتادن از پله‌ها باشد، در نظر بگیرید. الگوریتم برنامه‌ریزی حرکت این وظایف جداگانه را به عنوان ورودی می‌گیرد، فرمان سرعت و چرخش چرخ‌ها را تولید می‌کند و به ربات ارسال می‌کند. الگوریتم‌های برنامه‌ریزی حرکت ربات ممکن است با تعداد بیشتری از مفاصل (به عنوان مثال بازوهای صنعتی)، وظایفی پیچیده‌تر (به عنوان مثال دستکاری اشیاء)، محدودیت‌های مختلف (به عنوان مثال یک ماشین که فقط به جلو می‌تواند برود)، و عدم قطعیت (به عنوان مثال مدل ناقص محیط یا ربات) روبرو باشند.

برنامه‌ریزی حرکت دارای کاربردهای رباتیکی زیادی از قبیل خودمختاری، خودکارسازی، نرم‌افزار طراحی به وسیله کامپیوتر و نیز برنامه‌های کاربردی در زمینه‌های دیگر مانند پویانمایی شخصیت‌های دیجیتال، طراحی معماری، جراحی رباتیک و مطالعه مولکول‌های زیستی می‌باشد.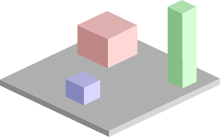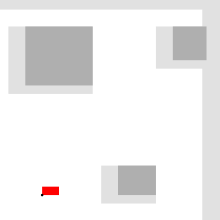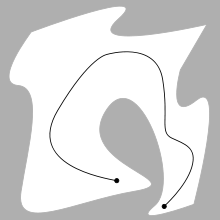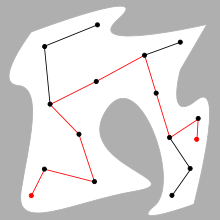

مسئلهٔ اصلی برنامه‌ریزی حرکت، تولید یک حرکت مداوم است که پیکربندی شروع S را به پیکربندی هدف G متصل کند، در حالی که از برخورد با موانع شناخته شده اجتناب کند. هندسهٔ ربات و موانع، در فضای کاری ۲ یا ۳ بعدی تعریف می‌شود. در حالی که حرکت، به عنوان یک مسیر (احتمالاً در ابعاد بالاتر) در فضای پیکربندی تعریف می‌شود.

یک پیکربندی، مکان روبات را تشریح می‌کند و فضای پیکربندی C، مجموعهٔ تمام پیکربندی‌های ممکن آن (تمام نقاطی که روبات امکان دستیابی به آن‌ها را دارد) می‌باشد. برای مثال:

• اگر ربات یک نقطه (بااندازه صفر) در صفحه ۲ بعدی باشد (فضای کار)،C یک صفحه می‌باشد و پیکربندی می‌تواند با استفاده از دو پارامتر(x,y) بیان شود.
• اگر ربات شی ای ۲بعدی باشد و بتواند حرکت و چرخش کند، فضای کار هنوز ۲ بعدی محسوب می‌شود با این حال،C گروه اقلیدسی خاصی به شرح زیر است:
  ${\displaystyle SE(2)=R^{2}*SO(2)}$
  (که (S0(2 یک گروه متعامد خاص، از حرکت‌های دوبعدی می‌باشد) واین پیکربندی می‌تواند با ۳ پارامتر (x, y, θ) نمایش داده شود.
• اگر ربات جسمی ۳ بعدی باشد که می‌تواند حرکت و چرخش کند، فضای کار ۳ بعدی است. اما C گروه اقلیدسی خاصی به شرح زیر است:
  ${\displaystyle SE(3)=R^{3}*SO(3)}$

و برای توصیف پیکربندی به ۶ پارامتر احتیاج است:(x, y, z):برای توصیف حرکت و (α, β, γ):برای زوایای اویلری.

• اگر ربات با پایه ثابت با N مفصل پیچیده (بدون حلقه‌های بسته) باشد، آنگاه C، از N بعد خواهد بود.

به مجموعه ای از پیکربندی‌ها که از برخورد با موانع جلوگیری می‌کنند، فضای خالی(C_free)می‌گوییم. مکمل C_freeرا C، موانع یا منطقه‌های ممنوعه، می‌نامیم. اغلب محاسبه شکل C_freeبسیار دشوار است، با این حال، آزمایش اینکه آیا یک پیکربندی داده شده در C_freeمی‌باشد یا نه، کارآمد می‌باشد. ابتدا با استفاده از کینماتیک به جلو، موقعیت هندسه ربات تعیین می‌شود و نمایانگر برخورد، برخورد موقعیت هندسی ربات با محیط را بررسی می‌کند.

فضای هدف یک زیر فضا از فضای آزاد است که ما می‌خواهیم ربات به آن جا برود. در برنامه‌ریزی حرکت جهانی (عمومی) فضای هدف مشاهده پذیر است. در حالی که در برنامه زیر حرکت محلی ممکن است فضای هدف مشاهده نشود. جهت حل مشکلات ناشی از مشاهده ناپذیری، چندین فضای هدف مجازی به نام فضای زیر هدف فرض می‌شود که در محل مشاهده پذیر واقع شده‌اند (پیرمامون ربات).^[۱]

مسائلی با ابعاد پایین، بوسیلهٔ الگوریتم‌های مبتنی بر شبکه، که این الگوریتم‌ها با استفاده از متصور شدن شبکه‌ای بر بالای فضای پیکربندی انجام می‌شوند، قابل حل هستند. این مسائل همچنین با استفاده از الگوریتم‌های هندسی که شکل و همبندی سی را محاسبه می‌کنند، قابل حل هستند. برنامه‌ریزی حرکت دقیق برای سیستم‌هایی با ابعاد بالاتر، تحت محدودیت‌ها و موانعی پیچیده، از لحاظ محاسباتی، مسئله ای رام نشدنی است. الگوریتم‌های میدان پتانسیل کارآمد هستند، اما این الگوریتم‌ها در کمترین مقدارهای ممکن محلی(local minima)، ناکارآمد هستند. الگوریتم‌های مبتنی برنمونه‌گیری از مشکل افتادن در مینیمم‌های محلی اجتناب می‌کنند و بسیاری از مسائل را نسبتاً سریع حل می‌کنند. با این حال، این الگوریتم‌ها قادر به تعیین این که هیچ راهی وجود ندارد نیستند، اما می‌توانند احتمال شکست در یافتن راه را محاسبه کنند که با سپری شدن زمان بیشتر، احتمال شکست را به صفر کاهش می‌دهند.

در حال حاضرالگوریتم‌های مبتنی بر نمونه‌گیری به روزترین و بهترین الگوریتم‌های برنامه‌ریزی حرکت برای فضاهایی با ابعاد بالا می‌باشند و حتی برای مسائلی با ده‌ها یا صدها بُعد، قابل پیاده‌سازی می‌باشند (مانند: بازوهای رباتیکی، مولکول‌های زیستی، انیمیشن کاراکترهای دیجیتال، روبات‌های دارای پا وغیره).

الگوریتم‌های مبتنی بر شبکه معمولاً شبکه‌ای را به صورت فرضی روی فضای پیکربندی قرار می‌دهند و فرض می‌کنند که هر پیکربندی با نقطه‌ای از نقاط شبکه مشخص می‌شود. در هر نقطه از این شبکه، ربات اجازه حرکت به نقطه مجاور را دارد به طوریکه خط بین نقطه شروع و پایان داخل C_freeباشد (این مسئله با استفاده از تشخیص برخورد، آزمایش می‌شود). مجموعهٔ این اعمال به همراه الگوریتم‌های جستجو (مانند A*) می‌توانند مسیری از مبدأ به سمت هدف را بیابند. این روش‌ها نیاز به تفکیک شبکه‌ای دارند. جستجو با شبکه‌های ضخیم‌تر، سریع‌تر می‌شود، اما در این حالت الگوریتم موفق به پیدا کردن مسیر از میان بخش‌های باریک C_free نمی‌شود. علاوه بر این، تعداد نقاط روی شبکه، در ابعاد فضای پیکربندی، رشد نمایی دارد که آنها را برای مسائلی با ابعاد بالا ناکارآمد می‌کند.

روش‌های سنتی مبتنی بر شبکه، مسیرهایی تولید می‌کنند که جهت تغییرات مسیر آنها محدود به مضاربی از زاویهٔ اولیهٔ داده شده می‌باشد. این روش‌ها اغلب منجر به ایجاد مسیرهایی می‌شوند که به‌طور جزئی بهینه هستند(solution suboptimal). هر کدام از روش‌های برنامه‌ریزی مسیر مبتنی بر زاویه، بدون اینکه مسیرشان را محدود به اضلاع شبکه کنند، مسیرهای کوتاه‌تری را با انتشار دادن اطلاعات در امتداد اضلاع شبکه پیدا می‌کنند. روش‌های مبتنی بر شبکه اغلب نیاز به جستجوی مداوم دارند، به عنوان مثال، زمانی که شناخت روبات از فضای پیکربندی تغییر کند یا خود فضای پیکربندی با پیدا کردن مسیرهایی تغییر کند. الگوریتم‌های جستجوی افزایشی اکتشافی، با استفاده از تجربه سایر مسائل مشابه برنامه‌ریزی مسیر-که قبلاً حل شده‌اند- با سرعت بالایی حرکت را برای مورد فعلی، برنامه‌ریزی می‌کنند.

این الگوریتم‌ها مبتنی بر یکی از ۲ حالت زیر می‌باشند:

- نمایش ربات در میان موانع چند ضلعی

• گراف قابل رویت بودن
• تجزیه المانی

- تعریف اشیا در میان موانع

• جمع مینکوسکی

در الگوریتم‌های پاداش محور فرض می‌شود ربات در هر حالت (موقعیت و حالت درونی) می‌تواند بین اعمال (حرکت) مختلف انتخاب کند. اگر چه نتیجه عمل به‌طور دقیق مشخص نیست. به عبارت دیگر درآمد پاره ای مبتنی بر تصادف و پاره مبتنی بر انتخاب ربات است. ربات وقتی به هدف می‌رسد پاداش مثبت دریافت می‌کند و وقتی به مانع برخورد می‌کند پاداش منفی می‌گیرد. این سری از الگوریتم‌ها درصدد یافتن مسیری هستند که مجموع پاداش‌های آتی را بیشینه نماید. فرایندهای تصمیم‌گیری مارکوف یک چارچوب ریاضی بسیار معروف است که در بسیاری از الگوریتم‌های پاداش محور استفاده می‌شود. مزیت استفاده از فرایندهای تصمیم‌گیری مارکوف نسبت به سایر الگوریتم‌های پاداش محور این است که مسیر بهینه را مشخص می‌کند. عیب فرایندهای تصمیم‌گیری مارکوف این است که ربات را به انتخاب عمل در بین مجموعه ای متناهی از اعمال محدود می‌کند و بنابراین مسیر نرم (هموار) نیست. فرایندهای تصمیم‌گیری مارکوف فازی یک بسط (توسعه) بر فرایندهای تصمیم‌گیری مارکوف است که با کمک سیستم‌های استنتاج فازی مسیر را هموار می‌کند^[۱]

یک روش برای برنامه‌ریزی حرکت، فرض کردن ربات به عنوان نقطه ای داخل میدانهای پتانسیل است. این روش کشش به سمت هدف و دافعه از موانع را با هم ترکیب می‌کند. خط سیر نهایی، خروجی به عنوان مسیر مدنظر می‌باشد. این روش با توجه به اینکه خط سیر با محاسبه کمی به‌دست می‌آید، مفید واقع می‌شود. اگرچه، این الگوریتم‌ها می‌توانند در مینیمم‌های محلی میدانهای پتانسیل به دام بیفتند و موفق به پیدا کردن مسیر نشوند. میدان پتانسیل می‌تواند به‌طور مستقیم از یک فرمول ریاضی (مانند میدان الکترواستاتیک) یا به کمک مجموعه ای از قوانین زبانی به دست آید^[۲]

الگوریتم‌های مبتنی بر نمونه‌گیری، فضای پیکربندی را با نقشه راهی از پیکربندی‌های از قبل نمونه‌گیری شده، نمایش می‌دهند. یک الگوریتم ابتدایی، N پیکره بندی را در فضای C نمونه‌گیری می‌کند و آن‌ها را در C_free، برای استفاده به عنوان نمونه شاخص نگه می‌دارند. سپس نقشه راه به گونه ای ساخته می‌شود که دو شاخص P و Q را، درصورتیکه بخش PQ کاملاً درون C_freeباشد، بهم متصل می‌کند. آنگاه الگوریتم تشخیص دهنده برخورد ،C_freeرا برای وجود برخورد بازبینی می‌کند. برای پیدا کردن مسیری که S و G را بهم متصل می‌کند، آنها نیر به نقشه راه، افزوده می‌شوند. اگر مسیر نقشه راه، بتواند G و S را بهم مرتبط کند، برنامه‌ریزی حرکت، موفق بوده‌است و و این مسیر را برمی‌گرداند. اگر جواب مثبتی پیدا نشود یا نمونه برداری کافی نیست یا راهی وجود ندارد.

این الگوریتم‌ها درفضای پیکربندی با ابعاد بالا بسیار خوب کار می‌کنند، چرا که برخلاف الگوریتم‌های ترکیبیاتی، زمان اجرای آنها به‌طور توانی، وابسته به ابعاد فضای پیکره بندی C نیست و همچنین دارای پیاده‌سازی اساساً ساده‌تری نیز می‌باشند. این الگوریتم‌ها از نظر احتمالی کامل هستند یعنی احتمال یافتن راه حل مسئله توسط این الگوریتم‌ها با گذر زمان به ۱ نزدیک می‌شود. با این حال، آنها نمی‌توانند عدم وجود راه حل برای مسئله را تعیین نمایند.

اثبات شده‌است که با داشتن موقعیت‌های میدان دید در C_free، هنگامیکه تعداد پیکربندی‌های N افزایش می‌یابد، احتمال اینکه الگوریتم ذکر شده راه حلی را بیابد، به‌طور توانی^[۳] به ۱ نزدیک می‌شود. میدان دید به‌طور صریح وابسته به ابعاد C نمی‌باشد؛ یعنی ممکن است که فضایی در ابعاد بالا با میدان دید خوب یا در ابعاد پایین با میدان دیدی ضعیف داشت. نتایج تجربی روش‌های مبتنی بر نمونه‌گیری، نشان می‌دهند که فضاهایی که به‌طور معمول، بیشتر دیده می‌شوند، میدان دید خوبی نیز دارند.

به یک برنامه‌ریز حرکت در صورتی کامل گفته می‌شود که همیشه زمانیکه مسیری درحالت کلی وجود دارد، یک مسیر ممکن را به درستی تولید کند. بیشتر الگوریتمهای کامل، مبتنی بر هندسه هستند. کارایی برنامه‌ریزهای کامل توسط نظریه پیچیدگی محاسباتی ارزیابی می‌شود.

کامل بودن از لحاظ تفکیک‌پذیری عامل دیگری است، بدین سان که اگر تفکیک‌پذیری شبکه ای که درنظر گرفته شده، به اندازه کافی ظریف باشد، یافتن مسیر توسط برنامه‌ریز حرکت، تضمین می‌شود. بیشتر برنامه‌ریزهایی که از لحاظ تفکیک‌پذیری کاملند، مبتنی بر شبکه می‌باشند. پیچیدگی محاسباتی این گونه برنامه‌ریزها وابسته به تعداد نقاط شبکه ای است که برای الگوریتم آن درنظر گرفته شده‌است. که این پیچیدگی (O(1/h^dخواهد بود که h تفکیک‌پذیری (طول یکی از اضلاع سلول شبکه) و d بعد فضای پیکر بندی می‌باشد.

کامل بودن احتمالاتی نیز ویژگی دیگری است بدین سان که احتمال اینکه برنامه‌ریز نتواند مسیری را پیدا کند (با اینکه مسیری وجود داشته)، درحالیکه کار بیشتری درحال انجام است، به‌طور مجانبی به صفر نزدیک می‌شود. کارایی برنامه‌ریزی که این ویژگی را دارد، با استفاده از میزان همگرایی، اندازه‌گیری می‌شود. برنامه‌ریزهای ناکامل همواره مسیری ممکن (وقتی مسیری وجود دارد) را تولید نمی‌کنند. اما گاهی برنامه‌ریزهای ناکامل نیز در عمل بسیار خوب عمل می‌کنند.

• برنامه‌ریزی دینامیک جنبشی (Kinodynamic planning)
• مسئله کوهنوردی (Mountain climbing problem)
• مانع سرعتی (Velocity obstacle)

در ویکی‌انبار پرونده‌هایی دربارهٔ برنامه‌ریزی حرکت موجود است.

• Jean-Claude Latombe talks about his work with robots and motion planning, 5 April ۲۰۰۰
• «کتابخانه استراتژی حرکت»، http://msl.cs.uiuc.edu/msl/
• «بسته ترجمه ماشینی»، http://ai.stanford.edu/~mitul/mpk
• «برنامه ریزی حرکت و کنترل ربات»، http://www.laas.fr/~jpl/book.html