|
Pertidaksamaan segitiga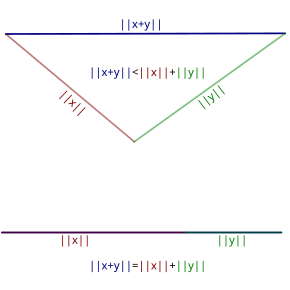 Dalam matematika, pertidaksamaan segitiga menyatakan bahwa untuk sebarang segitiga, jumlah panjang dua sisi haruslah lebih besar daripada panjang sisi yang lain.[1][2] Dalam geometri Euklides dan beberapa geometri lainnya ini adalah teorema. Dalam kasus Euklides, baik pada pernyataan lebih kecil atau sama dengan dan lebih besar atau sama dengan, kesamaan terjadi hanya jika segitiga memiliki sebuah sudut 180° dan dua sudut 0°, seperti yang ditunjukkan pada contoh bawah gambar di kanan. Ketidaksamaan tersebut dapat dilihat secara intuitif dalam R2 atau R3. Gambar di kanan menunjukkan dua contohnya Geometri Euklides Euklides membuktikan pertidaksamaan segitiga pada geometri bidang datar menggunakan konstruksi pada gambar.[3] Dengan menggunakan sebarang segitiga ABC, sebuah segitiga sama kaki dibentuk dengan sisi BC, dan kaki lain BD yang terletak pada perpanjangan garis AB. Dengan menunjukkan bahwa sudut β > α, dapat disimpulkan AD > AC. Namun AD = AB + BD = AB + BC, sehingga didapatkan AB + BC > AC. Bukti ini muncul dalam buku Element Euklides, Buku 1, Proposisi 20.[4] Daftar pustaka
|