Identitas (matematika)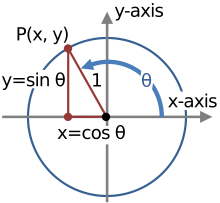

Dalam matematika, identitas adalah persamaan yang menghubungkan satu ekspresi matematika A ke ekspresi matematika lainnya B , sedemikian rupa sehingga A dan B (yang mungkin berisi beberapa variabel) menghasilkan nilai yang sama untuk semua nilai variabel dalam rentang validitas tertentu.^[1][2] Dengan kata lain, A = B adalah identitas jika A dan B sama dengan fungsi, dan identitas adalah persamaan antara fungsi yang didefinisikan secara berbeda. Misalnya, ${\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}}$ dan ${\displaystyle \cos ^{2}\theta +\sin ^{2}\theta =1}$ adalah identitas.^[2] Identitas terkadang ditunjukkan dengan simbol batang tiga ≡ daripada =, tanda sama dengan.^[3]

Identitas tertentu, khususnya ${\displaystyle a+0=a}$ dan ${\displaystyle a+(-a)=0}$, membentuk dasar aljabar,^[4] sedangkan identitas lainnya, misalnya ${\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}}$ dan ${\displaystyle (a+b)(a-b)=a^{2}-b^{2}}$, dapat berguna dalam menyederhanakan ekspresi aljabar dan mengembangkannya.^[5]

Secara geometris, identitas trigonometri adalah identitas yang melibatkan fungsi tertentu dari satu atau lebih sudut.^[6] Identitas tersebut berbeda dari identitas segitiga, yang merupakan identitas yang melibatkan sudut dan panjang sisi sebuah segitiga. Hanya yang pertama dibahas dalam artikel ini.

Identitas ini berguna setiap kali ekspresi yang melibatkan fungsi trigonometri perlu disederhanakan. Aplikasi penting lainnya adalah integrasi dari fungsi non-trigonometri: teknik umum yang melibatkan penggunaan aturan substitusi dengan fungsi trigonometri, dan kemudian menyederhanakan integral yang dihasilkan dengan identitas trigonometri.

Salah satu contoh paling menonjol dari identitas trigonometri melibatkan persamaan ${\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1,}$ yang benar untuk semua nilai kompleks dari ${\displaystyle \theta }$ (karena bilangan kompleks ${\displaystyle \mathbb {C} }$ membentuk domain sinus dan kosinus). Di sisi lain, persamaannya

${\displaystyle \cos \theta =1}$

hanya berlaku untuk nilai tertentu ${\displaystyle \theta }$, tidak semua (atau untuk semua nilai dalam lingkungan). Misalnya, persamaan ini benar jika ${\displaystyle \theta =0,}$ tapi salah saat ${\displaystyle \theta =2}$.

Kelompok lain dari identitas trigonometri menyangkut apa yang disebut rumus penjumlahan/pengurangan (misalnya identitas sudut ganda ${\displaystyle \sin(2\theta )=2\sin \theta \cos \theta }$, rumus penjumlahan untuk ${\displaystyle \tan(x+y)}$),^[3][1] yang dapat digunakan untuk memecah ekspresi sudut yang lebih besar menjadi ekspresi dengan konstituen yang lebih kecil.

Identitas berikut berlaku untuk semua eksponen bilangan bulat, asalkan basisnya bukan nol:

${\displaystyle {\begin{aligned}b^{m+n}&=b^{m}\cdot b^{n}\\(b^{m})^{n}&=b^{m\cdot n}\\(b\cdot c)^{n}&=b^{n}\cdot c^{n}\end{aligned}}}$

Tidak seperti penjumlahan dan perkalian, eksponen tidak komutatif. Sebagai contoh, 2 + 3 = 3 + 2 = 5 dan 2 · 3 = 3 · 2 = 6, melainkan 2³ = 8, sedangkan 3² = 9.

Dan tidak seperti penjumlahan dan perkalian, eksponen juga tidak asosiatif. Sebagai contoh, (2 + 3) + 4 = 2 + (3 + 4) = 9 dan (2 · 3) · 4 = 2 · (3 · 4) = 24, melainkan 2³ ke 4 adalah 8⁴ (atau 4.096), sedangkan 2 banding 3⁴ adalah 2⁸¹ (atau 2,417,851,639,229,258,349,412,352). Tanpa tanda kurung untuk mengubah urutan kalkulasi, menurut konvensi urutannya top-down, bukan bottom-up:

${\displaystyle b^{p^{q}}=b^{(p^{q})}\neq (b^{p})^{q}=b^{(p\cdot q)}=b^{p\cdot q}.}$

Beberapa rumus penting, terkadang disebut identitas logaritmik atau hukum log , menghubungkan logaritma satu sama lain.^[7]

Logaritma dari suatu perkalian adalah jumlah dari logaritma dari angka-angka yang dikalikan; logaritma rasio dua bilangan adalah selisih logaritma. Logaritma dari p kekuatan angka adalah p kali logaritma dari angka itu sendiri; logaritma dari a-p root adalah logaritma bilangan dibagi dengan p . Tabel berikut mencantumkan identitas ini dengan contoh. Setiap identitas dapat diturunkan setelah substitusi definisi logaritma x = b^log_b(x), and/or y = b^log_b(y), di sisi kiri.

	Formula	Contoh
produk	${\displaystyle \log _{b}(xy)=\log _{b}(x)+\log _{b}(y)}$	${\displaystyle \log _{3}(243)=\log _{3}(9\cdot 27)=\log _{3}(9)+\log _{3}(27)=2+3=5}$
hasil bagi	${\displaystyle \log _{b}\!\left({\frac {x}{y}}\right)=\log _{b}(x)-\log _{b}(y)}$	${\displaystyle \log _{2}(16)=\log _{2}\!\left({\frac {64}{4}}\right)=\log _{2}(64)-\log _{2}(4)=6-2=4}$
pangkat	${\displaystyle \log _{b}(x^{p})=p\log _{b}(x)}$	${\displaystyle \log _{2}(64)=\log _{2}(2^{6})=6\log _{2}(2)=6}$
akar	${\displaystyle \log _{b}{\sqrt[{p}]{x}}={\frac {\log _{b}(x)}{p}}}$	${\displaystyle \log _{10}{\sqrt {1000}}={\frac {1}{2}}\log _{10}1000={\frac {3}{2}}=1.5}$

Logaritma log_b(x) dapat dihitung dari logaritma x dan b sehubungan dengan basis sembarang k menggunakan rumus berikut:

${\displaystyle \log _{b}(x)={\frac {\log _{k}(x)}{\log _{k}(b)}}.}$

Biasanya kalkulator ilmiah menghitung logaritma ke basis 10 dan e .^[8] Logaritma yang terkait dengan basis b apa pun dapat ditentukan menggunakan salah satu dari dua logaritma ini dengan rumus sebelumnya:

${\displaystyle \log _{b}(x)={\frac {\log _{10}(x)}{\log _{10}(b)}}={\frac {\log _{e}(x)}{\log _{e}(b)}}.}$

Diberikan angka x dan logaritma log_b(x) ke basis yang tidak diketahui b , basis diberikan oleh:

${\displaystyle b=x^{\frac {1}{\log _{b}(x)}}.}$

Fungsi hiperbolik memenuhi banyak identitas, semuanya mirip bentuknya dengan identitas trigonometri. Faktanya, Kaidah Osborn^[9] menyatakan bahwa seseorang dapat mengubah identitas trigonometri apa pun menjadi identitas hiperbolik dengan mengembangkannya sepenuhnya dalam hal kekuatan integral sinus dan cosinus, mengubah sinus menjadi sinh dan cosinus menjadi cosh, dan mengganti tanda setiap suku yang berisi hasil kali 2, 6, 10, 14, ... sinh.^[10]

Fungsi Gudermannian memberikan hubungan langsung antara fungsi melingkar dan fungsi hiperbolik yang tidak melibatkan bilangan kompleks.

Dalam logika matematika dan dalam aljabar universal, identitas didefinisikan sebagai rumus dari bentuk "∀x₁,...,x_n. s = t", di mana s dan t adalah istilah tanpa variabel bebas selain x₁,...,x_n. The quantifier prefix ("∀x₁,...,x_n.") sering dibiarkan implisit, khususnya dalam aljabar universal. Misalnya, aksioma dari monoid sering diberikan sebagai identitas himpunan

{   ∀x,y,z. x*(y*z)=(x*y)*z   ,   ∀x. x*1=x   ,   ∀x. 1*x=x   },

atau, dalam notasi singkatnya, sebagai

{   x*(y*z)=(x*y)*z   ,   x*1=x   ,   1*x=x   }.

Beberapa penulis menggunakan nama "persamaan" daripada "identitas".^[11][12]

• Identitas akuntansi
• Daftar identitas matematika

Wikimedia Commons memiliki media mengenai Identity (mathematics).

• The Encyclopedia of Equation Online encyclopedia of mathematical identities (archived)
• A Collection of Algebraic Identities Diarsipkan 2011-10-01 di Wayback Machine.