|
Produk (teori kategori)Dalam teori kategori, produk dari dua (atau lebih) objek dalam kategori adalah gagasan yang dirancang untuk esensi di balik konstruksi di bidang matematika lain seperti produk himpunan Kartesius, produk langsung dari grup atau gelanggang, dan produk dari ruang topologi. Pada dasarnya, produk dari suatu keluarga objek adalah objek "paling umum" untuk morfisme untuk setiap objek yang diberikan. DefinisiProduk dari dua objekMemperbaiki kategori C. Misalkan X1 dan X2 menjadi objek C. Hasil perkalian dari X1 dan X2 adalah objek X, dilambangkan dengan X1 × X2, sepasang morfisme π1 : X → X1, π2 : X → X2 menggunakan sifat universal berikut:
![Properti[pranala nonaktif permanen] universal produk](http://upload.wikimedia.org/wikipedia/commons/thumb/8/89/CategoricalProduct-03.svg/280px-CategoricalProduct-03.svg.png) Keberadaan produk tergantung pada C atau X1 dan X2 . Jika tidak ada, untuk isomorfisma kanonik, karena sifat universal, jadi satu adalah tentang produk. Morfisme π1 dan π2 disebut proyeksi kanonik atau morfisme proyeksi. Dengan Y dan f1 f2 morfisme f disebut produk dari morfisme f1 dan f2 dilambangkan ⟨f1, f2⟩. Produk dari keluarga arbitasiDua objek, dengan kumpulan objek arbitasi yang diindeks oleh himpunan I. Dengan keluarga objek (Xi)i∈I, produk dari keluarga merupakan objek X dengan morfisme πi : X → Xi dengan sifat universal berikut:
![Produk[pranala nonaktif permanen] universal produk](http://upload.wikimedia.org/wikipedia/commons/thumb/3/37/Cat_product.svg/149px-Cat_product.svg.png) Produk dilambangkan sebagai Πi∈I Xi . Jika I = {1, ..., n }, maka dilambangkan X1 × ... × Xn X1 × ... × Xn X1 × ... × Xn X1 × ... × Xn dan produk dari morfisme dilambangkan ⟨ f1, ..., fn ⟩. Definisi persamaanAtau, produk didefinisikan melalui persamaan. Jadi, misalnya, untuk produk biner:
Sebagai limitProduk adalah kasus khusus dengan limit. Dilihat dengan menggunakan kategori diskrit (keluarga objek tanpa morfisme, selain morfisme identitas) sebagai diagram diperlukan untuk definisi limit. Objek diskrit berfungsi sebagai indeks komponen dan proyeksi. Jika kita menganggap diagram ini sebagai funktor, funktor dari himpunan indeks I anggap sebagai kategori terpisah. Definisi produk kemudian bertepatan dengan definisi batas, { f }i adalah kerucut dan proyeksi menjadi batas (kerucut limit). Sifat universalSebagaimana limit adalah kasus khusus dari konstruksi universal, begitu pula produknya. Dimulai dengan definisi yang diberikan untuk sifat universal dari limit, ambillah J sebagai kategori diskrit dengan dua objek, sehingga CJ adalah produk kategori C × C Fungsi diagonal Δ : C → C × C denganpasangan berurutan (X, X) ke setiap objek X dan morfisme f pasangan (f, f) . Produk X1 × X2 dalam C diberikan oleh morfisme universal dari functor Δ ke objek (X1, X2) dalam C × C Morfisme universal ini terdiri dari objek X dari C dan morfisme (X, X) → (X1, X2) yang berisi proyeksi. ContohDalam kategori himpunan, produk (dalam pengertian teoretis kategori) adalah produk Kartesius. Diberikan keluarga himpunan Xi produk didefinisikan sebagai
dengan proyeksi kanonik
Diberikan setiap himpunan Y dengan keluarga fungsi fi : Y → Xi, panah universal f : Y → Πi∈I Xi didefinisikan oleh f(y) : = (fi(y))i∈I Contoh lain:
DiskusiContoh dimana produk tidak ada: Dalam kategori bidang, produk Q × Fp tidak ada, karena tidak ada bidang dengan homomorfisme untuk Q dan Fp. Contoh lain: Produk kosong (misal I adalah himpunan kosong) sama dengan objek terminal, dan beberapa kategori, seperti kategori grup tak hingga, tidak memiliki objek terminal: mengingat grup G tak hingga ada banyak morfisme ℤ → G, jadi G tidak bisa menjadi terminal. Jika I adalah himpunan sehingga semua produk untuk keluarga indeks dengan I, maka dapat memperlakukan setiap produk sebagai funktor CI → C [2] Bagaimana fungsi ini memetakan objek sudah jelas. Pemetaan morfisme tidak kentara, karena produk morfisme yang didefinisikan di atas tidak sesuai. Pertama, pertimbangkan fungsi produk biner, yang merupakan bifunktor. Untuk f1 : X1 → Y1, f2 : X2 → Y2 maka mencari morfisme X1 × X2 → Y1 × Y2 . Dengan memilih ⟨ f1 o π1, f2 o π2 ⟩. Operasi morfisme ini disebut produk morfisme kartesian.[3] Kedua, pertimbangkan fungsi produk umum. Untuk keluarga {X}i,{Y}i, fi : Xi → Yi kita harus menemukan morfisme Πi∈I Xi → Πi∈I Yi . Kami memilih produk dari morfisme {fi o πi}i . Kategori dimana setiap himpunan objek hingga memiliki produk kadang-kadang disebut kategori kartesian[4] (meskipun beberapa penulis menggunakan frasa ini untuk berarti "kategori dengan semua batas terbatas"). Produk bersifat asosiatif. Misalkan C adalah kategori kartesian, fungsi produk telah dipilih seperti di atas, dan 1 menunjukkan objek terminal C Kami kemudian memiliki isomorfisme alami. Sifat ini secara formal dengan sifat monoid komutatif; kategori kartesius dengan produk hingga adalah contoh kategori monoidal simetris. DistributivitasUntuk setiap objek X, Y, dan Z dari kategori dengan produk hingga dan produk bersama, terdapat morfisme kanonik X × Y + X × Z → X × (Y + Z), dimana tanda tambah di sini menunjukkan koproduk. Untuk melihat ini, perhatikan bahwa sifat universal dari produk bersama X × Y + X × Z keberadaan panah diagram berikut (panah induksi): 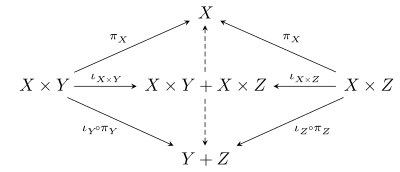 Sifat universal dari produk X × (Y + Z) kemudian menjamin morfisme X × Y + X × Z → X × (Y + Z) disebabkan oleh panah pada diagram di atas. Kategori distributif adalah kategori di mana morfisme ini sebenarnya adalah isomorfisme. Jadi dalam kategori distributif isomorfisme kanonik
Lihat pula
Referensi
Pranala luar
|



