|
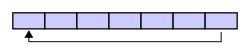
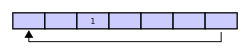
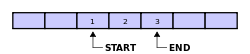
Penyangga melingkar Dalam ilmu komputer, penyangga melingkar, antrean melingkar, penyangga siklis, atau penyangga cincin adalah struktur data yang menggunakan sebuah penyangga tunggal dengan ukuran terdefinisi yang menghubungkan ujung memori ke awal memori, sehingga seolah tak memiliki ujung.[1] Gambaran umum Sebuah penyangga melingkar awalnya kosong dan memiliki panjang yang terdefinisi. Diagram berikut memiliki tujuh elemen penyangga: Asumsikan bahwa 1 ditulis di tengah penyangga melingkar (posisi awalnya tidak penting): Lalu, asumsikan bahwa dua elemen lain ditambahkan ke penyangga melingkar— 2 & 3—setelah elemen 1: Bila dua elemen dihapus, maka dua elemen tertua dalam penyangga melingkar akan dihapus. Struktur data ini menggunakan logika FIFO (first in, first out) yang menyatakan bahwa data yang lebih dahulu masuk akan lebih dahulu keluar. Pada contoh di atas, dikarenakan 1 & 2 adalah elemen yang lebih dahulu memasuki penyangga melingkar, maka mereka yang akan dihapus — menyisakan elemen 3. Jika penyangga memiliki tujuh elemen (sesuai panjang penyangga di atas), maka penyangga dianggap penuh: Apabila penyangga melingkar sudah penuh dan dilakukan penulisan data setelahnya, maka data yang paling tua akan ditimpa. Pada contoh kita, dua elemen tambahan yakni A & B ditambahkan sehingga menimpa elemen 3 & 4. Alternatif lain untuk mencegah penimpaan data adalah mengembalikan pesan error atau memunculkan pengecualian. Perihal apakah data akan ditimpa atau tidak bergantung kepada aplikasi yang menggunakan penyangga melingkar. Terakhir, jika kita menghapus dua elemen, maka yang terhapus adalah 5 & 6. Hal ini dikarenakan 5 & 6 menjadi elemen tertua pada penyangga melingkar, sehingga hasil akhirnya adalah: PenggunaanKarakteristik paling berguna dari penyangga melingkar adalah fakta bahwa elemen di dalamnya tidak harus disusun ulang ketika kita melakukan penghapusan data (berbeda dengan penyangga nonmelingkar yang mengharuskan kita menggeser seluruh elemen). Dalam kata lain, penyangga melingkar cocok sebagai penyangga FIFO (first in, first out), sementara penyangga nonmelingkar cocok sebagai penyangga LIFO (last in, first out). Penyangga sirkuler merupakan strategi implementasi yang baik untuk antrean dengan ukuran terdefinisi. Namun, jika kita ingin mengubah ukuran penyangga melingkar, maka kita perlu menggeser memori yang cukup boros. Bila kita perlu mengubah ukuran antrean, maka pendekatan senarai berantai bisa jadi lebih cocok. Pada situasi tertentu, penyangga melingkar yang menimpa data lama bisa digunakan, misalnya dalam kasus multimedia. Bila penyangga digunakan sebagai penyangga berbatas di masalah produsen-konsumen, maka produsen (misal generator audio) mungkin menginginkan penimpaan data jika konsumen (misal kartu audio) tidak mampu mengimbangi. Mekanisme penyangga melingkar Sebuah penyangga melingkar dapat diimplementasikan dengan sebuah pointer dan tiga integer:[2]
Diagram berikut menunjukkan penyangga hampir penuh dengan panjang = 7: Diagram berikut menunjukkan penyangga penuh yang telah ditimpa: Pada awal dibuat, indeks awal dan indeks akhir akan diatur menjadi 0. Kemudian, penulisan penyangga melingkar akan menulis data ke indeks akhir dan indeks akhir digeser ke posisi penyangga berikutnya. Penyangga melingkar akan membaca elemen dari indeks awal kemudian digeser ke posisi penyangga berikutnya. Informasi mengenai indeks awal dan akhir saja tidak cukup untuk menentukan apakah penyangga penuh atau kosong jika seluruh slot digunakan.[3] Namun, hal tersebut dapat diatasi dengan membatasi penggunaan buffer hingga sejumlah Panjang - 1.[4] Dalam kasus ini, penyangga dianggap kosong jika indeks awal dan akhir bernilai sama dan penuh jika ukuran terisinya Panjang - 1. Solusi lainnya adalah dengan menyimpan integer yang bertambah nilainya ketika operasi tulis dilakukan dan berkurang jika operasi baca dilakukan. Pengecekan dapat dilakukan dengan membaca nilai integer tadi, jika bernilai 0 maka kosong, sementara jika bernilai sama dengan panjang maka penuh.[5] Berikut adalah contoh implementasi penyangga melingkar sederhana. Fungsi put() menempatkan data di penyangga, sementara fungsi get() mengambil data dari penyangga. Kedua fungsi akan mengurus kapasitas penyangga: #include <stdio.h>
enum { N = 10 }; // Elemen N dari penyangga melingkar
int buffer [N]; // Ingat bahwa ukuran aslinya adalah N-1, perhatikan fungsi put()
int writeIndx = 0;
int readIndx = 0;
int put (int item)
{
if ((writeIndx + 1) % N == readIndx)
{
// penyangga penuh, hindari luberan
return 0;
}
buffer[writeIndx] = item;
writeIndx = (writeIndx + 1) % N;
return 1;
}
int get (int * value)
{
if (readIndx == writeIndx)
{
// penyangga kosong
return 0;
}
*value = buffer[readIndx];
readIndx = (readIndx + 1) % N;
return 1;
}
int main ()
{
// uji penyangga melingkar
int value = 1001;
while (put (value ++));
while (get (& value))
printf ("read %d\n", value);
return 0;
}
Referensi
|