Metode Hartree–Fock

Dalam kimia dan fisika komputasi, metode Hartree–Fock (HF) merupakan suatu metode hampiran untuk menentukan fungsi gelombang dan energi dari sistem benda-banyak kuantum dalam keadaan stasioner. Metode ini merupakan suatu prosedur pengulangan "swapanggah" (self-consistent) untuk menghitung "kemungkinan terbaik" penyelesaian determinan tunggal terhadap persamaan Schrödinger tak gayut-waktu dari sistem berelektron banyak dalam potensial Coulomb inti tetap. Sebagai akibatnya, walaupun cara ini menghitung energi pertukaran secara tepat, metode ini sama sekali tidak menghitung pengaruh korelasi elektron. Karena inti dimodelkan sebagai titik-titik muatan yang diam, metode ini hanya dapat diterapkan setelah dilakukan pendekatan Born–Oppenheimer.

Metode Hartree–Fock terkadang mengasumsikan bahwa fungsi gelombang benda-N yang pasti pada sistem dapat dihampiri melalui suatu determinan Slater tunggal (dalam kasus apabila partikelnya adalah fermion) atau melalui suatu permanen tunggal (untuk kasus boson) pada orbital spin N. Dengan mengoperasikan metode variasional, maka dapat diperoleh satu set N-pasang persamaan bagi orbital spin N. Penyelesaian bagi persamaan tersebut menghasilkan fungsi gelombang Hartree–Fock dan energi sistem tersebut.

Khususnya dalam beberapa literatur lama, metode Hartree–Fock disebut pula sebagai metode medan swapanggah (self-consistent field; SCF). Dengan menurunkan persamaan yang saat ini dikenal sebagai persamaan Hartree sebagai penyelesaian hampiran bagi persamaan Schrödinger, Hartree memerlukan medan akhir yang dimasukkan dari distribusi muatan agar dapat "swapanggah" dengan medan awal yang diasumsikan. Dengan demikian, swapanggah adalah persyaratan dari penyelesaian ini. Penyelesaian bagi persamaan Hartree–Fock non-linear juga berperilaku layaknya tiap partikel dikenai medan purata yang dibuat oleh seluruh partikel yang lain (lihat operator Fock di bawah) dan karenanya, terminologi tersebut berlanjut. Persamaan ini hampir secara universal diselesaikan melalui suatu metode iteratif, walaupun algoritma iterasi titik tetap tidak selalu konvergen.^[1] Skema penyelesaian ini bukanlah satu-satunya penyelesaian yang mungkin dan bukan merupakan fitur penting dari metode Hartree–Fock.

Metode Hartree–Fock tidak hanya digunakan dalam penyelesaian persamaan Schrödinger bagi atom, molekul, struktur nano^[2] dan padatan namun juga digunakan dalam fisika nuklir. (Lihat metode Hartree–Fock–Bogoliubov untuk diskusi penerapannya dalam teori struktur nuklir). Dalam teori struktur atom, perhitungan dimungkinkan bagi suatu spektrum dengan banyak aras tenaga tereksitasi dan karenanya metode Hartree–Fock bagi atom mengasumsikan fungsi gelombang dalam suatu fungsi keadaan konfigurasi dengan bilangan kuantum yang terdefinisi dengan baik serta bahwa aras tenaga tidak selalu merupakan keadaan dasar.

Nama metode ini diambil dari nama Douglas Hartree yaitu ilmuwan yang menemukan metode "metode medan swapanggah", dan Vladimir A. Fock yang menunjukkan ketepatan logika metode Hartree dan merumuskannya kembali menjadi bentuk matriks yang digunakan hingga sekarang.

Metode Hartree–Fock umumnya digunakan untuk menyelesaikan persamaan Schrödinger tak gayut-waktu bagi suatu atom atau molekul banyak-elektron seperti dijelaskan dalam pendekatan Born–Oppenheimer. Karena tidak ada penyelesaian yang diketahui bagi sistem banyak-elektron (terdapat penyelesaian bagi sistem satu-elektron seperti atom hidrogenik dan kation hidrogen diatomik), permasalahan tersebut diselesaikan secara numerik. Karena nonlinearitas diperkenalkan oleh pendekatan Hartree–Fock, persamaan-persamaannya diselesaikan menggunakan metode nonlinear seperti iterasi, yang kemudian menghasilkan penamaan "metode medan swapanggah."

Metode Hartree–Fock membuat lima penyederhanaan utama untuk menangani tugas ini:

• Pendekatan Born–Oppenheimer secara inheren diasumsikan. Fungsi gelombang molekul penuh sebenarnya adalah fungsi dari koordinat masing-masing inti, selain dari elektron.
• Biasanya, efek relativistik sama sekali diabaikan. Operator momentum diasumsikan sepenuhnya non-relativistik.
• Penyelesaian variasional diasumsikan sebagai kombinasi linear dari sejumlah fungsi basis terbatas, yang biasanya (tetapi tidak selalu) dipilih menjadi ortogonal. Basis set diasumsikan agar mendekati lengkap.
• Setiap eigenfungsi energi diasumsikan dapat dijelaskan oleh determinan Slater tunggal, produk antisimetris dari fungsi gelombang satu elektron (misalnya orbital).
• pendekatan medan purata tersirat. Efek yang timbul dari penyimpangan asumsi ini diabaikan. Efek-efek ini sering secara kolektif digunakan sebagai definisi dari istilah korelasi elektron. Namun, label "korelasi elektron" yang diucapkan secara ketat mencakup korelasi Coulomb dan korelasi Fermi, dan yang terakhir adalah efek pertukaran elektron, yang sepenuhnya diperhitungkan dalam metode Hartree-Fock.^[3][4] Dinyatakan dalam terminologi ini, metode ini hanya mengabaikan korelasi Coulomb. Namun, ini adalah kelemahan penting, yang menyebabkan (antara lain) ketidakmampuan Hartree-Fock untuk menangkap dispersi London.^[5]

Relaksasi dari dua perkiraan terakhir menimbulkan apa yang kemudian disebut sebagai metode pasca-Hartree–Fock.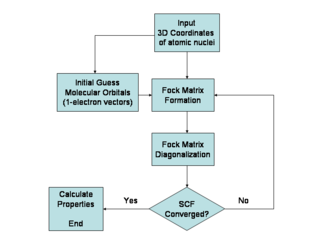

Titik awal dari metode Hartree–Fock adalah sekumpulan orbital-orbital hampiran. Untuk perhitungan atom, orbital hampiran ini biasanya merupakan orbital atom bakhidrogen (suatu atom berelektron satu, tapi dengan muatan inti yang disesuaikan). Untuk perhitungan molekul atau kristal, fungsi gelombang hampiran awal merupakan kombinasi linear orbital-orbital atom. Hal ini menghasilkan kumpulan orbital-orbital berelektron satu yang, karena sifat fermion elektron, harus antisimetris; sifat antisimetri ini diperoleh dengan menggunakan determinan Slater.

Hamiltonian benda-banyak (many-body Hamiltonian) digunakan untuk memodelkan interaksi antara elektron dan inti,

${\displaystyle {\hat {H}}=\sum _{i}{-{\frac {1}{2}}\nabla _{i}^{2}}-\sum _{i}{\sum _{a}{\frac {Z_{a}}{\left|\mathbf {r_{i}} -\mathbf {d_{a}} \right|}}}+{\frac {1}{2}}\sum _{i}{\sum _{j\neq i}{\frac {1}{\left|\mathbf {r_{i}} -\mathbf {r_{j}} \right|}}}+{\frac {1}{2}}\sum _{a}{\sum _{b\neq a}{\frac {Z_{a}Z_{b}}{\left|\mathbf {d_{a}} -\mathbf {d_{b}} \right|}}}}$

di mana ${\displaystyle \mathbf {r_{i}} }$ merupakan vektor posisi dari elektron ${\displaystyle i}$ dengan komponen-komponen vektor dalam jari-jari Bohr, ${\displaystyle Z_{a}}$ merupakan muatan inti yang diam (${\displaystyle a}$) dalam satuan muatan elementer, dan ${\displaystyle \mathbf {d_{a}} }$ merupakan vektor posisi dari inti ${\displaystyle a}$ dengan komponen vektor dalam jari-jari Bohr.

Suku awal dalam Hamiltonian adalah penjumlahan operator-operator energi kinetik untuk masing-masing elektron di dalam sistem. Hal kedua adalah penjumlahan tarikan Coulomb elektron-inti. Hal ketiga adalah penjumlahan tolakan Coulomb elektron-elektron. Hal akhir adalah penjumlahan tolakan Coulomb inti-inti, juga dikenal sebagai energi tolakan inti. Karena Hampiran Born–Oppenheimer telah dibuat, dan operator tolakan inti tidak dipengaruhi oleh posisi elektron, dapat dihitung sekali diawal prosedur Hartree-Fock dan kemudian diperlakukan sebagai konstanta dipengaruhi hanya oleh posisi inti.

Secara khusus, dalam perhitungan Hartree–Fock modern, fungsi gelombang dihampiri sebagai perkalian dari fungsi-fungsi gelombang satu-elektron, yang kemudian dihampiri melalui kombinasi linear orbital-orbital atom. Lebih lanjut, sangat umum untuk orbital atom yang digunakan untuk digabungkan melalui kombinasi linear dari satu atau lebih fungsi tipe-Gaussian, daripada menggunakan orbital tipe-Slater, dalam menghemat waktu perhitungan. Hampiran dari fungsi gelombang dengan cara ini dapat diperoleh dengan menggunakan persamaan Roothaan, yang menghampiri Hamiltonian sesungguhnya dari sistem.

Setelah fungsi gelombang dibangun, elektron kemudian dipilih. Dampak dari semua elektron yang lain dijumlahkan dan digunakan untuk membangun potensial. (Inilah mengapa prosedur ini terkadang disebut sebagai prosedur medan purata). Ini memberikan elektron tunggal dengan potensial tertentu, di mana persamaan Schrödinger dapat dipecahkan, memberikan sedikit perbedaan fungsi gelombang untuk elektron tersebut. Proses ini kemudian diulang untuk setiap elektron yang lain, yang menyelesaikan satu tahap prosedur. Prosedur keseluruhan kemudian diulang, sampai perubahan dari satu tahap ke tahap lainnya cukup kecil.

Kestabilan numerik dapat menjadi masalah untuk prosedur ini—banyak cara untuk memerangi ketidakstabilan ini. Salah satu yang cukup dasar dan secara umum dapat diterapkan disebut dengan F-mixing (pencampuran-F). Dengan pencampuran-F, sekali fungsi gelombang elektron tunggal dihitung, dia tidak digunakan secara langsung. Malahan, beberapa kombinasi dari fungsi gelombang yang dihitung dan fungsi gelombang sebelumnya untuk elektron tersebut digunakan – yang paling umum adalah kombinasi linear dari yang dihitung dan dengan segera fungsi gelombang sebelumnya. Sebuah pengelakan yang pintar, digunakan oleh Hartree, untuk perhitungan atomik adalah dengan meningkatkan muatan inti,yang menarik semua elektron menjadi berdekatan. Dengan distabilkannya sistem, ini setahap demi setahap dikurangi ke muatan yang sesungguhnya.

Alternatif untuk perhitungan Hartree–Fock yang digunakan dalam beberapa kasus adalah teori fungsi rapatan, yang memberikan baik energi korelasi maupun pertukaran tetapi tidak didasarkan secara murni pada pemecahan mekanika kuantum. Tentu saja, cukup umum untuk menggunakan perhitungan yang merupakan gabungan antara dua metode. Sebagai contoh yang cukup terkenal adalah pola B3LYP. Perhitungan Hartree-Fock dapat digunakan sebagai titik awal untuk metode yang lebih mendalam, seperti teori gangguan badan-banyak (many-body perturbation)

• Gaussian
• Gamess
• NWChem
• Q-Chem
• MPQC

• Levine, Ira N. (1991). Quantum Chemistry (dalam bahasa Inggris) (edisi ke-4). Englewood Cliffs, New Jersey: Prentice Hall. hlm. 455–544. ISBN 0-205-12770-3. 
• Cramer, Christopher J. (2002). Essentials of Computational Chemistry (dalam bahasa Inggris). Chichester: John Wiley & Sons, Ltd. hlm. 153–189. ISBN 0-471-48552-7. 
• Szabo, A.; Ostlund, N. S. (1996). Modern Quantum Chemistry (dalam bahasa Inggris). Mineola, New York: Dover Publishing. ISBN 0-486-69186-1. 

• (Inggris) "The Wave Mechanics of an Atom with a Non-Coulomb Central Field. Part II. Some Results and Discussion" oleh D. R. Hartree, Mathematical Proceedings of the Cambridge Philosophical Society, Volume 24, 111-132, Januari 1928
• (Inggris) An Introduction to Hartree-Fock Molecular Orbital Theory oleh C. David Sherrill (Juni 2000)
• (Inggris) "Mean-Field Theory: Hartree-Fock and BCS" dalam E. Pavarini, E. Koch, J. van den Brink, dan G. Sawatzky: Quantum materials: Experiments and Theory, Jülich 2016, ISBN 978-3-95806-159-0