Jarak Hamming

Jarak Hamming pada kubus biner 3-bit

Dua contoh jarak: Titik 100 dan 011 berjarak 3; sedangkan titik 010 dan 111 berjarak 2.

Jarak minimum antar dua titik pada kubus adalah jarak Hamming antara dua string biner.

Dalam teori informasi, jarak Hamming antara dua string dengan panjang yang sama, adalah banyaknya posisi di kedua string yang berbeda simbol.^[1] Dalam kata lain, jarak Hamming mengukur minimum banyaknya subtitusi yang dibutuhkan untuk mengubah satu string menjadi string lain. Dalam konteks yang lebih umum, jarak Hamming adalah salah satu metriks untuk mengukur edit distance antara dua barisan. Jarak ini dinamai dengan nama matematikawan Amerika, Richard Hamming.

Jarak ini sering digunakan di teori kode, lebih spesifik pada kode blok, dengan string dengan panjang sama berupa vektor atas finite field.

Simbol pada string dapat berupa karakter, bit, digit desimal, maupun hal-hal lain. Berikut adalah contoh jarak Hamming antara:

• "karolin" dan "kathrin" adalah 3.
• "karolin" dan "kerstin" adalah 3.
• "kathrin" dan "kerstin" adalah 4.
• 1011101 dan 1001001 adalah 2.
• 2173896 dan 2233796 adalah 3.

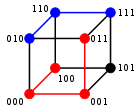
Untuk panjang n yang tetap, jarak Hamming adalah metrik pada himpunan kata dengan panjang n (juga dikenal sebagai ruang Hamming), karena memenuhi kondisi sifat ketaknegatifan, simetri, bernilai 0 jika dan hanya jika kedua kata identik, dan memenuhi ketaksamaan segitiga:^[2] untuk setiap kata a, b, dan c, jika terdapat perbedaan huruf ke-i di a dan huruf ke-i di c, maka setidaknya terdapat perbedaan huruf ke-i di a dan huruf ke-i di b, atau perbedaan huruf ke-i di c dan huruf ke-i di b. Karenanya, jarak Hamming antara a dan c tidak mungkin lebih besar dari jumlah jarak Hamming antara a dan b dan antara b dan c. Jarak Hamming antara kata a dan b juga dapat dipandang sebagai berat Hamming dari a - b -- untuk pemilihan operator (-) yang cocok, mirip seperti selisih nilai antara dua bilangan dapat dipandang sebagai jarak dari 0 pada garis bilangan.^{[butuh klarifikasi]}

Untuk untai biner a dan b, jarak Hamming sama dengan banyaknya 1 di a XOR b.^[3] Ruang metrik dari untai biner dengan panjang n, dan dengan jarak Hamming, dikenal dengan kubus Hamming; hal ini setara dengan ruang metrik jarak antar himpunan titik di graf hiperkubus. String biner dengan panjang n juga dapat dipandang sebagai vektor di ${\displaystyle \mathbb {R} ^{n}}$dengan menganggap setiap simbol sebagai koordinat. Dengan embedding ini, string membentuk himpunan titik hiperkubus dimensi-n, dan jarak Hamming antar string setara dengan jarak Manhattan antar titik.

Jarak Hamming minimum digunakan untuk mendefinisikan beberapa notasi penting pada teori kode, seperti kode pendeteksi galat dan kode pengoreksi galat. Secara khusus, suatu kode C dikatakan pendeteksi k-galat, jika dan hanya jika jarak Hamming minimum antara dua katakodenya setidaknya k+1.

Sebagai contoh, jarak Hamming antara katakode "000" dan "111" adalah 3, dan karenanya termasuk pendeteksi 2-galat. Hal ini berarti galat masih dapat terdeteksi jika sebuah atau dua bit berganti tanda. Namun jika tiga bit berganti tanda, "000" akan berubah menjadi "111" dan galat tidak dapat dideteksi.

Suatu kode C dikatakan pengoreksi k-galat bila, untuk setiap kata w di ruang Hamming H yang bersangkutan, terdapat paling banyak satu katakode c (elemen C) sehingga jarak Hamming antara w dan c tidak lebih dari k. Dengan kata lain, sebuah kode disebut pengoreksi k-galat jika dan hanya jika jarak Hamming minimum antara dua katakodenya adalah 2k+1. Hal ini dapat dipahami secara geometris dengan mengamati bola dengan radius k dan berpusat pada setiap katakode tidak dapat beririsan. Dalam konteks ini, bola tersebut juga disebut dengan bola Hamming.

Sebagai contoh, perhatikan kode tiga bit dari katakode "000" dan "111". Ruang Hamming-nya terdiri dari delapan kata 000, 001, 010, 100, 011, 101, 110, dan 111. Kodekata "000" dan kata dengan satu bit galat "001", "010", "100" memiliki jarak Hamming ke "000" yang tidak lebih dari 1. Dengan alasan yang serupa, katakode "111" dan kata dengan satu bit galat "110","101" and "011" memiliki jarak Hamming maksimal 1 dari katakode asli "111". Dalam kode ini setiap galat satu bit selalu memiliki 1 jarak Hamming dengan kodekata aslinya, karenanya kode termasuk pengoreksi 1-galat (yakni dengan k=1). Jarak Hamming minimum antara "000" dan "111" adalah 3, yang memenuhi 2k+1 = 3.

Dengan demikian jarak Hamming minimum d antar katakode dapat mendeteksi paling banyak d-1 galat dan dapat mengoreksi paling banyak ⌊(d-1)/2⌋ galat. Nilai terakhir ini juga disebut dengan radius packing atau kapabilitas pengoreksi galat dari kode.

Jarak ini dinamai dengan nama Richard Hamming, yang memperkenalkan konsep tersebut pada papernya "Error detecting and error correcting codes", di tahun 1950.^[4] Analisis bit dengan berat Hamming digunakan dalam beberapa disiplin ilmu, termasuk didalamnya teori informasi, teori kode, dan kriptografi.

Jarak ini digunakan dalam telekomunikasi untuk mengestimasi galat, dengan menghitung banyaknya bit yang berubah pada sebuah pesan dengan panjang konstan. Dalam konteks tersebut, jarak Hamming juga disebut dengan jarak sinyal.^[5]

Jarak Hamming juga digunakan dalam sistematika untuk mengukur jarak genetik.^[6]

Jarak Hamming bukan metrik yang baik untuk mengukur jarak dua string dengan panjang yang berbeda, atau ketika penyisipan dan penghapusan (selain subtitusi) karakter juga perlu dipertimbangkan. Definisi jarak Levenshtein lebih cocok pada kasus ini.

Fungsi berikut, ditulis dalam Python 3.7, menghasilkan jarak Hamming antara dua string:

def hamming_distance(string1, string2):
	dist_counter = 0
	for n in range(len(string1)):
		if string1[n] != string2[n]:
			dist_counter += 1
	return dist_counter

Atau dalam ekspresi yang lebih singkat

sum(xi != yi for xi, yi in zip(x, y))

1. ^ Waggener, Bill; Waggener, William N.; Waggener, William M. (1995). Pulse Code Modulation Techniques (dalam bahasa Inggris). Springer Science & Business Media. hlm. 206. ISBN 978-0-442-01436-0.  Parameter |url-status= yang tidak diketahui akan diabaikan (bantuan)
2. ^ Robinson, Derek John Scott. (2003). An introduction to abstract algebra. New York: Walter de Gruyter. hlm. 255–257. ISBN 3-11-019816-9. OCLC 567824926.  Parameter |url-status= yang tidak diketahui akan diabaikan (bantuan)
3. ^ Warren, Henry S. (2013). Hacker's delight (edisi ke-2nd ed). Upper Saddle River, NJ: Addison-Wesley. hlm. 81–96. ISBN 978-0-321-84268-8. OCLC 808684338.  Parameter |url-status= yang tidak diketahui akan diabaikan (bantuan)Pemeliharaan CS1: Teks tambahan (link)
4. ^ Hamming, R. W. (1950-04). "Error detecting and error correcting codes". The Bell System Technical Journal. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. ISSN 0005-8580.  Periksa nilai tanggal di: |date= (bantuan)
5. ^ Integrated circuit and system design : power and timing modeling, optimization and simulation : 22nd International Workshop, PATMOS 2012, Newcastle upon Tyne, UK, September 4-6, 2012, Revised selected papers. Ayala, Jose L., Shang, Delong., Yakovlev, Alex. Berlin: Springer. 2013. hlm. 62. ISBN 978-3-642-36157-9. OCLC 824738653.  Parameter |url-status= yang tidak diketahui akan diabaikan (bantuan)
6. ^ Pilcher, Christopher D.; Wong, Joseph K.; Pillai, Satish K. (2008 Mar 18). "Inferring HIV Transmission Dynamics from Phylogenetic Sequence Relationships". PLOS Medicine (dalam bahasa Inggris). 5 (3): e69. doi:10.1371/journal.pmed.0050069. ISSN 1549-1676. PMC 2267810 . PMID 18351799.  Periksa nilai tanggal di: |date= (bantuan)Pemeliharaan CS1: Format PMC (link)