|
Barisan harmonik (matematika)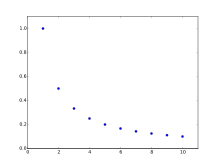 Dalam matematika, progresi harmonik (atau barisan harmonik) adalah sebuah barisan yang diambil dari invers perkalian dari suatu barisan aritmatika. Secara sederhana, deret harmonik adalah barisan yang kebalikannya membentuk barisan aritmatika. Ekuivalennya, suatu barisan disebut barisan harmonik jika setiap suku merupakan rata-rata harmonik dari suku-suku tetangganya. Sebagai karakterisasi ekuivalen yang ketiga, barisan harmonik adalah urutan takhingga dari bentuk di mana a adalah bilangan bukan nol dan −a/d adalah bukan suatu bilangan asli, atau suatu barisan berhingga dari bentuk di mana a adalah bilangan bukan nol, k adalah suatu bilangan asli, dan −a/d adalah bukan suatu bilangan asli atau lebih besar dari k. ContohBerikut ini n adalah suatu bilangan asli, secara berurut:
Jumlah dari barisan harmonikBarisan harmonik tidak terbatas tidak dapat dijumlahkan (karena penjumlahannya takhingga). Tidak mungkin suatu barisan harmonik dari pecahan satuan yang berbeda (selain dari kasus trivial di mana a = 1 dan k = 0) akan menghasilkan bilangan bulat. Alasannya adalah setidaknya satu penyebut dari deret tersebut akan habis dibagi oleh suatu bilangan prima yang tidak habis dibagi penyebut lainnya.[1] Penggunaan dalam geometriJika titik-titik kolinier A, B, C, dan D sedemikian sehingga D adalah konjugat harmonik dari C terhadap A dan B, maka jarak dari salah satu titik ini ke tiga titik lainnya membentuk barisan harmonik.[2][3] Secara khusus, masing-masing barisan AC, AB, AD; BC, BA, BD; CA, CD, CB; dan DA, DC, DB adalah barisan harmonik, di mana masing-masing jarak ditandai berdasarkan orientasi garis yang tetap. Dalam sebuah segitiga, jika garis tinggi segitiga berada dalam barisan aritmatika, maka sisi-sisinya berada dalam progresi harmonik. Menara miring LireContoh yang sangat bagus dari barisan harmonik adalah Menara miring Lire. Di dalamnya, balok-balok yang seragam ditumpuk di atas satu sama lain untuk mencapai jarak menyamping atau lateral maksimum yang cukup. Balok-balok tersebut ditumpuk 1/2, 1/4, 1/6, 1/8, 1/10, … dengan jarak menyamping di bawah balok asli atau sebelumnya. Hal ini memastikan bahwa pusat gravitasi berada tepat di tengah-tengah menara sehingga tidak runtuh. Sedikit saja penambahan berat pada menara akan menyebabkan menara menjadi tidak stabil dan runtuk. Lihat juga
Referensi
|








