Analisis frekuensi

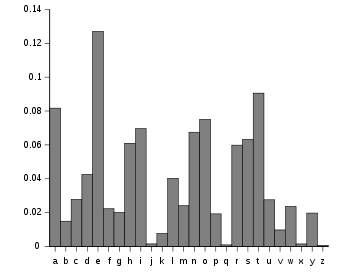Dalam analisis kriptografi, analisis frekuensi (juga dikenal sebagai menghitung huruf) merupakan studi dari frekuensi huruf atau kelompok huruf dalam teks tersandi. Metode ini digunakan untuk membantu memecahkan sandi klasik.

Analisis frekuensi berdasarkan fakta bahwa, dalam bentangan bahasa tulisan tertentu, huruf atau kombinasi huruf tertentu terjadi dengan frekuensi yang bervariasi. Selain itu, terdapat distribusi karakteristik huruf yang is kira-kira sama untuk hampir semua sampel dari bahasa itu. Misalnya, diketahui bagian dari Bahasa Inggris, E, T, A, dan O paling sering digunakan, sedangkan Z, Q, X, dan J jarang digunakan. Demikian juga TH, ER, ON, dan AN adalah pasangan huruf yang paling sering digunakan (disebut bigram atau digraph), serta SS, EE, TT, dan FF merupakan huruf berulang yang paling sering digunakan.^[1] Frasa tak masuk akal "ETAOIN SHRDLU" mewakili 12 huruf yang paling sering digunakan dalam teks Bahasa Inggris yang tipikal.

Dalam beberapa sandi, sifat-sifat teks terang dari bahasa alami dipertahankan dalam teks sandi, dan pola-pola ini berpotensi diekspoitasi dalam serangan khusus teks sandi.

Dalam sandi substitusi sederhana, setiap huruf dari teks terang diganti dengan huruf yang lain, dan huruf tertentu dalam teks terang akan selalu diganti menjadi huruf yang sama dalam teks sandi. Misalnya, jika semua jumlah huruf e diubah menjadi huruf X, pesan teks sandi yang berisi banyak huruf X akan membuat analis kriptografi bahwa X mewakili e.

Penggunaan dasar dari analisis frekuensi adalah pertama-tama untuk menghitung frekuensi huruf teks sandi dan kemudian menebak mengasosiasikan huruf teks terang yang ditebak dengan huruf tersebut. Lebih banyak X dalam teks sandi daripada huruf yang lain menyimpulkan bahwa X berkaitan dengan e dalam teks terang, tetapi contoh ini tidak pasti benar; t dan a juga huruf yang paling banyak digunakan dalam Bahasa Inggris, jadi X mungkin juga bermakna huruf tersebut. Kecil kemungkinan huruf X menjadi z atau q yang jarang digunakan pada teks terang. Sehingga analis kriptografi mungkin perlu mencoba beberapa kombinasi pemetaan antara huruf-huruf dalam teks sandi dan teks terang.

Penggunaan statistik yang lebih kompleks dapat dipahami, seperti mempertimbangkan jumlah pasangan huruf (bigrams), triplet (trigrams), dan seterusnya. Ini dilakukan untuk memberikan lebih banyak informasi bagi analis kriptografi, misalnya, Q dan U hampir selalu muncul bersama secara berurutan dalam Bahasa Inggris, meski Q sendiri jarang digunakan.

Misalnya Eve telah menerima kriptogram di bawah ini, dan diketahui teks ini terenkripsi menggunakan sandi substitusi sederhana sebagai berikut:

LIVITCSWPIYVEWHEVSRIQMXLEYVEOIEWHRXEXIPFEMVEWHKVSTYLXZIXLIKIIXPIJVSZEYPERRGERIM
WQLMGLMXQERIWGPSRIHMXQEREKIETXMJTPRGEVEKEITREWHEXXLEXXMZITWAWSQWXSWEXTVEPMRXRSJ
GSTVRIEYVIEXCVMUIMWERGMIWXMJMGCSMWXSJOMIQXLIVIQIVIXQSVSTWHKPEGARCSXRWIEVSWIIBXV
IZMXFSJXLIKEGAEWHEPSWYSWIWIEVXLISXLIVXLIRGEPIRQIVIIBGIIHMWYPFLEVHEWHYPSRRFQMXLE
PPXLIECCIEVEWGISJKTVWMRLIHYSPHXLIQIMYLXSJXLIMWRIGXQEROIVFVIZEVAEKPIEWHXEAMWYEPP
XLMWYRMWXSGSWRMHIVEXMSWMGSTPHLEVHPFKPEZINTCMXIVJSVLMRSCMWMSWVIRCIGXMWYMX

Untuk contoh ini, huruf kapital digunakan untuk menandakan teks sandi, huruf kecil digunakan untuk menandakan teks terang (atau tebakan), dan X~t digunakan untuk menyatakan tebakan bahwa huruf teks sandi X merepresentasikan huruf teks terang t.

Eve dapat menggunakan analisis frekuensi untuk membantu memecahkan pesan melalui kalimat-kalimat berikut: jumlah huruf dalam kriptogram menunjukkan bahwa I merupakan huruf tunggal yang paling banyak muncul,^[2] XL merupakan bigram yang paling banyak muncul, dan XLI merupakan trigram yang paling banyak muncul. e merupakan huruf yang paling sering digunakan dalam Bahasa Inggris, th merupakan bigram yang paling sering digunakan, dan the merupakan trigram yang paling sering digunakan. Ini menyimpulkan bahwa X~t, L~h and I~e. Huruf terbanyak kedua dalam kriptogram adalah E; karena huruf tersering pertama dan kedua dalam Bahasa Inggris adalah e dan t, Eve menebak bahwa E~a, huruf tersering ketiga. Dengan menggunakan asumsi sementara ini, maka pesan dekripsi parsial diperoleh sebagai berikut.

heVeTCSWPeYVaWHaVSReQMthaYVaOeaWHRtatePFaMVaWHKVSTYhtZetheKeetPeJVSZaYPaRRGaReM
WQhMGhMtQaReWGPSReHMtQaRaKeaTtMJTPRGaVaKaeTRaWHatthattMZeTWAWSQWtSWatTVaPMRtRSJ
GSTVReaYVeatCVMUeMWaRGMeWtMJMGCSMWtSJOMeQtheVeQeVetQSVSTWHKPaGARCStRWeaVSWeeBtV
eZMtFSJtheKaGAaWHaPSWYSWeWeaVtheStheVtheRGaPeRQeVeeBGeeHMWYPFhaVHaWHYPSRRFQMtha
PPtheaCCeaVaWGeSJKTVWMRheHYSPHtheQeMYhtSJtheMWReGtQaROeVFVeZaVAaKPeaWHtaAMWYaPP
thMWYRMWtSGSWRMHeVatMSWMGSTPHhaVHPFKPaZeNTCMteVJSVhMRSCMWMSWVeRCeGtMWYMt

Dengan menggunakan tebakan awal ini, Eve dapat menempatkan pola yang mengonfirmasikan pilihannya, seperti "that". Selain itu, pola-pola lainnya menyimpulkan tebakan-tebakan yang lain. "Rtate" dapat berarti "state", yang berarti R~s. "atthattMZe" juga dapat ditebak sebagai "atthattime", yang menghasilkan M~i dan Z~m. Lebih lanjut lagi, "heVe" dapat berarti "here", sehingga V~r. Dengan tebakan tersebut, Eve memperoleh:

hereTCSWPeYraWHarSseQithaYraOeaWHstatePFairaWHKrSTYhtmetheKeetPeJrSmaYPassGasei
WQhiGhitQaseWGPSseHitQasaKeaTtiJTPsGaraKaeTsaWHatthattimeTWAWSQWtSWatTraPistsSJ
GSTrseaYreatCriUeiWasGieWtiJiGCSiWtSJOieQthereQeretQSrSTWHKPaGAsCStsWearSWeeBtr
emitFSJtheKaGAaWHaPSWYSWeWeartheStherthesGaPesQereeBGeeHiWYPFharHaWHYPSssFQitha
PPtheaCCearaWGeSJKTrWisheHYSPHtheQeiYhtSJtheiWseGtQasOerFremarAaKPeaWHtaAiWYaPP
thiWYsiWtSGSWsiHeratiSWiGSTPHharHPFKPameNTCiterJSrhisSCiWiSWresCeGtiWYit

Selanjutnya, tebakan ini menyimpulkan kata yang lain (misalnya, "remarA" dapat berarti "remark", sehingga A~k) dan seterusnya, dan relatif mudah untuk menyimpulkan huruf-huruf lainnya, yang pada akhirnya menghasilkan teks terang.

hereuponlegrandarosewithagraveandstatelyairandbroughtmethebeetlefromaglasscasei
nwhichitwasencloseditwasabeautifulscarabaeusandatthattimeunknowntonaturalistsof
courseagreatprizeinascientificpointofviewthereweretworoundblackspotsnearoneextr
emityofthebackandalongoneneartheotherthescaleswereexceedinglyhardandglossywitha
lltheappearanceofburnishedgoldtheweightoftheinsectwasveryremarkableandtakingall
thingsintoconsiderationicouldhardlyblamejupiterforhisopinionrespectingit

Pada tahap ini, mungkin ide yang bagus bagi Eve untuk menyisipkan spasi dan tanda baca:

Hereupon Legrand arose, with a grave and stately air, and brought me the beetle
from a glass case in which it was enclosed. It was a beautiful scarabaeus, and, at
that time, unknown to naturalists—of course a great prize in a scientific point
of view. There were two round black spots near one extremity of the back, and a
long one near the other. The scales were exceedingly hard and glossy, with all the
appearance of burnished gold. The weight of the insect was very remarkable, and,
taking all things into consideration, I could hardly blame Jupiter for his opinion
respecting it.

Dalam contoh dari The Gold-Bug ini, tebakan Eve semuanya tepat. Namun ini tidak akan selalu terjadi; variasi dalam statistika untuk teks terang individual dapat berarti bahwa tebakan awalnya tidak tepat. Mungkin perlu melakukan backtracking pada tebakan yang tidak tepat atau untuk menganalisis statistika yang tersedia secara lebih mendalam daripada pembenaran yang agak disederhanakan yang diberikan dalam contoh di atas.

Hal itu juga memungkinkan bahwa teks terang tidak menunjukkan distribusi frekuensi huruf yang diharapkan. Pesan yang lebih singkat mungkin menampilkan lebih banyak variasi. Hal itu juga memungkinkan untuk membentuk skewed text secara artifisial. Misalnya, seluruh isi novel yang ditulis tanpa huruf "e" — suatu bentuk literatur yang dikenal sebagai lipogram.

Penjelasan analisis frekuensi (dalam hal analisis kriptografi) didokumentasikan pertama kali pada abad ke-9 oleh Al-Kindi, seorang ahli polimatik Arab, dalam A Manuscript on Deciphering Cryptographic Messages.^[3] Hal ini disimpulkan bahwa studi tekstual dekat pada Al-Qur'an pertama kali mengungkapkan bahwa Bahasa Arab memiliki frekuensi huruf karakteristik.^[4] Penggunaannya menyebar, dan sistem serupa digunakan secara luas di negara-negara Eropa pada masa Renaisans. Pada 1474, Cicco Simonetta telah menulis sebuah manual dalam memecahkan enkripsi dalam teks berbahasa Latin dan Italia text.^[5]

Beberapa skema ditemukan oleh para kriptografer untuk mengatasi kelemahan dalam enkripsi substitusi sederhana. Hal ini termasuk:

• Substitusi homofon: Penggunaan homophones — beberapa alternatif untuk huruf yang paling umum dalam penyandian substitusi monoalfabetik. Misalnya, untuk Bahasa Inggris, teks sandi X dan Y mungkin berarti teks terang E.
• Substitusi polialfabetik, yang merupakan penggunaan beberapa alfabet — dipilih dalam cara yang beragam dan lebih atau kurang licik (Leone Alberti tampaknya telah menjadi yang pertama yang menggagas metode ini); dan
• Substitusi Poligrafik, skema di mana pasangan atau triplet huruf teks terang diperlakukan sebagai kesatuan untuk substitusi, alih-alih huruf tunggal, misalnya Sandi Playfair yang ditemukan oleh Charles Wheatstone pada pertengahan abad ke-19.

Kerugian dari semua upaya ini untuk mengalahkan serangan penghitungan frekuensi adalah bahwa metode ini is that it meningkatkan kerumitan penyandian dan penguraian, sehingga terjadi kesalahan. Misalnya, seorang Sekretaris Luar Negeri Britania disebut telah menolak sandi Playfair karena bahkan jika anak se bahkan jika anak sekolah dapat mengatasinya dengan sukses seperti yang ditunjukkan Wheatstone dan Playfair, "atase kami tidak akan pernah bisa mempelajarinya!".

Mesin rotor pada pertengahan pertama dari abad ke-20 (misalnya mesin Enigma) pada dasarnya kebal terhadap analisis frekuensi langsung. Namun, jenis ("serangan") analisis lainnya berhasil membaca sandi pesan dari sebagian dari mesin ini.

Analisis frekuensi hanya memerlukan pemahaman dasar dari statistika bahasa teks terang dan beberapa keterampilan penyelesaian masalah, dan, jika dilakukan secara manual, toleransi untuk pembukuan huruf yang luas. Selama Perang Dunia II, Britania Raya dan Amerika Serikat merekrut para pemecah kode dengan menempatkan teka-teki silang di surat kabar utama dan mengadakan kontes bagi yang dapat menyelesaikannya paling cepat. Beberapa penyandi yang digunakan oleh blok Poros dipecahkan menggunakan analisis frekuensi, misalnya, sebagian penyandi konsuler digunakan oleh Jepang. Metode mekanis penghitungan huruf dan analisis statistik (umumnya mesin jenis kartu IBM) pertama kali digunakan dalam Perang Dunia II, kemungkinan oleh SIS tentara Amerika Serikat. Saat ini, kerja keras penghitungan dan analisis huruf telah digantikan oleh perangkat lunak komputer, yang dapat melakukan analisis tersebut dalam hitungan detik. Dengan kekuatan komputasi modern, penyandi klasik tidak mungkin memberikan perlindungan nyata untuk data rahasia.

Analisis frekuensi telah dideskripsikan dalam fiksi. "The Gold-Bug" karya Edgar Allan Poe, dan kisah Sherlock Holmes "The Adventure of the Dancing Men" karya Sir Arthur Conan Doyle merupakan contoh dari kisah yang mendeskripsikan penggunaan analisis frekuensi untuk menyerang penyandi substitusi sederhana. Penyandi dalam kisah Poe bertatahkan dengan beberapa tindakan penipuan, tetapi ini lebih ke perangkat yang literer dibandingkan apapun yang signifikan secara kriptografis.

• Helen Fouché Gaines, "Cryptanalysis", 1939, Dover. ISBN 0-486-20097-3
• Abraham Sinkov, "Elementary Cryptanalysis: A Mathematical Approach", The Mathematical Association of America, 1966. ISBN 0-88385-622-0.

1. ^ Singh, Simon. "The Black Chamber: Hints and Tips". Diakses tanggal 26 October 2010. 
2. ^ "A worked example of the method from bill's "A security site.com"". Diarsipkan dari versi asli tanggal 2013-10-20. Diakses tanggal 2012-12-31.  Parameter |url-status= yang tidak diketahui akan diabaikan (bantuan)
3. ^ Ibrahim A. Al-Kadi "The origins of cryptology: The Arab contributions", Cryptologia, 16(2) (April 1992) pp. 97–126.
4. ^ "In Our Time: Cryptography". BBC Radio 4. Diakses tanggal 29 April 2012. 
5. ^ Kahn, David L. (1996). The codebreakers: the story of secret writing. New York: Scribner. ISBN 0-684-83130-9. 

• Alat analisis frekuensi daring
• Frekuensi karakter dan suku kata dari 41 bahasa dan alat portabel untuk membuat distribusi frekuensi dan suku kata
• Analisis frekuensi huruf Arab
• Probabilitas bersyarat untuk karakter dalam teks Bahasa Inggris
• Frekuensi huruf/bigram/trigram Ceko